Introducción
La optimización es un campo de estudio amplio y muy interesante. Mis primeras interacciones con este campo empezaron jugueteando con regresiones lineales y usando el clásico descenso del gradiente, programado manualmente. No solo resulta satisfactorio desde el punto de vista teórico, sino que también es extremadamente útil en la práctica. Cuando hablamos de optimización, la idea principal que suele venirnos a la cabeza es la de realizar una tarea de la mejor manera posible, utilizando la menor cantidad de recursos.
En nuestro día a día, que suele ser bastante ajetreado, todos intentamos optimizar distintos procesos cotidianos: limpiar, cocinar, desplazarnos, estudiar o trabajar, entre otros. De forma consciente o no, tomamos decisiones orientadas a ahorrar tiempo, esfuerzo o dinero, lo que constituye un ejemplo claro de optimización aplicada a la vida diaria.
En el ámbito del comercio, la optimización es un elemento casi inherente al propio sistema capitalista (al menos en su formulación teórica más ideal). Las empresas compiten entre sí tratando de ofrecer mejores bienes y servicios, y esta competencia actúa como motor para la mejora continua de los procesos. Por ejemplo, si una empresa de reparto de paquetes consigue realizar sus envíos de forma más rápida y utilizando menos combustible que otra, podrá ofrecer precios más competitivos. Al reducir el consumo de recursos, esta empresa más eficiente puede mantener (o incluso aumentar) su margen de beneficio frente a otra cuyo proceso logístico sea menos eficiente.
Este tipo de situaciones ilustran claramente problemas de optimización. En el caso del transporte, existen múltiples rutas posibles entre distintos destinos, pero no todas son igualmente buenas. El objetivo es encontrar el recorrido óptimo en función de ciertas variables, como el tráfico en un momento determinado, la existencia de obras, la distancia entre puntos de entrega o el consumo de combustible. La optimización permite modelar este problema y determinar, entre todas las alternativas posibles, aquella que minimiza el coste total o maximiza la eficiencia del proceso.
Dentro de este campo de estudio, existen multitud de herramientas matemáticas y de métodos para optimizar un problema. Como breve resumen, enumeraré algunos de los enfoques más usados:
- Algoritmos basados en gradiente: utilizan información de derivadas de la función objetivo para guiar la búsqueda hacia óptimos locales o globales. Son muy eficientes cuando la función es continua y diferenciable (por ejemplo, descenso por gradiente o métodos de Newton).
- Metaheurísticas: métodos de búsqueda aproximada inspirados en procesos naturales o estrategias probabilísticas. No garantizan el óptimo global, pero son muy útiles en problemas complejos, no lineales o discontinuos. En este blog hablaré sobre los algoritmos genéticos, el ejemplo más básico de metaheurística.
- Métodos exactos: técnicas matemáticas que garantizan encontrar la solución óptima, como la programación lineal, entera o convexa. Suelen ser computacionalmente costosos y aplicables solo a problemas con una estructura bien definida.
- Métodos heurísticos: estrategias diseñadas específicamente para un tipo de problema concreto, que priorizan la rapidez frente a la optimalidad. Son comunes en problemas de gran escala o en tiempo real.
Para poder definir un problema general como un problema de optimización, es necesario establecer ciertos elementos fundamentales que lo definan de manera clara y precisa. Matemáticamente, y de forma simplificada, un problema de optimización tiene esta forma:
\[\begin{aligned} \text{Función objetivo a minimizar} \quad & f(x) \\ \text{sujeto a} \quad & g_j(x) \le 0, \quad j = 1,2,\ldots,s, \\ & h_j(x) = 0, \quad j = 1,2,\ldots,w, \\ & x_i, \quad i = 1,2,\ldots,n. \end{aligned}\]De forma resumida, tenemos una función que queremos minimizar o maximizar, junto con una serie de restricciones que hay que cumplir. En el ejemplo del transportista, lo que queremos es gastar el menor combustible posible, pero con la condición de que no podemos pasar por las calles $x$ e $y$ debido a las obras, y de que hay que visitar todas las casas del recorrido.
A continuación explicaré brevemente algunos conceptos que son indispensables para entender el diseño de los métodos de optimización.
Conceptos clave
Función fitness
Esta función establece una forma de evaluar soluciones para nuestro problema. Es una forma de cuantificar el rendimiento. También puede ser vista como una forma de cuantificar un error. En ese caso, deberíamos minimizarla.
Óptimos globales y locales
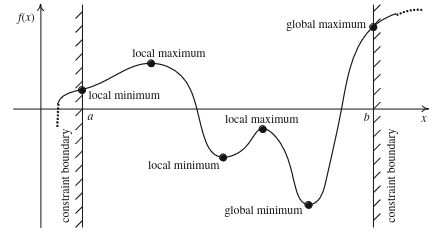
Imaginemos una función como una superficie en $3D$, quizá semejante a una cadena montañosa, con picos y llena de valles y depresiones. Así es más sencillo entender estos conceptos. Encontrar el óptimo global correspondería a encontrar el punto más bajo de toda la superficie, el valle más profundo de la región. En la búsqueda por descender lo máximo posible, es posible quedarse atrapado en depresiones menos profundas que, en relación con su entorno inmediato, son las más bajas. Estos son los óptimos locales.
Un senderista que se mueve por este terreno no tiene una visión completa del paisaje. Solo percibe la pendiente inmediata que le rodea. Su estrategia es simple: avanzar siempre cuesta abajo.
Siguiendo esta regla, el senderista acabará llegando a un punto donde todas las direcciones cercanas ascienden. Desde su punto de vista, ha alcanzado el fondo del valle: cualquier paso que dé lo hará subir. Sin embargo, ese punto puede no ser el lugar más bajo de toda la región, sino solo el más bajo en su entorno inmediato. Ese punto corresponde a un óptimo local.
Algunos métodos topan con la misma problemática del senderista. Se quedan atascados en valores subóptimos.
Dentro de todos los métodos de optimización existentes, hay unos que son bastante divertidos e interesantes. Son fáciles de programar, intuitivos y generalmente funcionan muy bien. Estas son las llamadas metaheurísticas, métodos cuya principal característica es la aleatoriedad como motor principal de exploración. Y concretamente dentro de estos algoritmos, voy a hablar de los algoritmos genéticos.
Algoritmos genéticos
La premisa es básica. Esta familia de algoritmos se inspira en las ideas de Darwin sobre la evolución, más concretamente, en los mecanismos de selección natural y supervivencia del más apto, donde los individuos mejor adaptados al entorno tienen mayor probabilidad de reproducirse y transmitir sus características a la siguiente generación.
Estos sistemas (y todas las metaheurísticas) tienen dos fases generales de vital importancia y muy sensibles. La exploración y la explotación.
Exploración y explotación
Como he mencionado antes, la aleatoriedad es una parte clave de estas técnicas. Esta característica permite explorar zonas del espacio que quizá no habrían sido visitadas en primera instancia por parecer menos prometedoras. Gracias a ello, se permite una exploración más amplia y se facilita escapar de óptimos locales. Esta primera fase de búsqueda es la conocida como exploración.
La explotación viene justo después. Esta es la habilidad de refinar y ajustar lo máximo posible una zona de soluciones, encontrando la mejor solución posible dentro de esta.
El balance entre ambas fases es muy sensible y es necesario ajustarlo con finura. Si la exploración dominase, el algoritmo tardaría mucho tiempo en conseguir una solución, o incluso no convergería a ninguna. En cambio, si la explotación fuese más fuerte que la exploración, la convergencia sería muy prematura y posiblemente se encontraría una solución subóptima, cuando podría haber muchas mejores opciones sin descubrir.
Los algoritmos genéticos son capaces de explorar y explotar gracias a su variada selección de operadores. Aunque, antes de profundizar en detalles sobre estos, hay que entender el algoritmo de forma general.
Las GAs trabajan con una población de soluciones codificadas normalmente en forma binaria. Cada solución, llamada cromosoma, está compuesta por genes (bits), y el conjunto de cromosomas constituye la población. Esta población se inicializa de manera aleatoria para favorecer la exploración del espacio de soluciones y, posteriormente, cada cromosoma es evaluado según su calidad, lo que hace posible ordenar las soluciones de mejor a peor. A partir de esta evaluación comienza el proceso evolutivo, que se desarrolla en generaciones. En cada generación se seleccionan los cromosomas más aptos para reproducirse, sin eliminar completamente la diversidad.
Los operadores genéticos principales son el cruce, que combina información de dos progenitores para generar nuevas soluciones, y la mutación, que introduce cambios aleatorios para evitar la convergencia prematura. El operador de selección es también importante, pues es el encargado de indicar qué cromosomas deben cruzarse entre sí. También es posible añadir una mecánica de elitismo, para mejorar la convergencia. Con apoyo del elitismo, que preserva las mejores soluciones, este ciclo se repite hasta cumplir un criterio de parada, tomando finalmente el mejor cromosoma como solución aproximada al problema. A continuación proporciono un diagrama general del ciclo evolutivo:
graph TD
A[Inicio] --> B[Inicializar población aleatoria]
B --> C[Evaluar fitness de toda la población]
C --> D[Ordenar por fitness]
D --> E{¿Iteración < max_iter?}
E -->|No| P[Retornar mejor solución]
E -->|Sí| F[Seleccionar élites]
F --> G{¿Población completa?}
G -->|No| H[Selección por ruleta]
H --> I[Crossover de padres]
I --> J[Mutación de hijos]
J --> K[Agregar hijos a nueva población]
K --> G
G -->|Sí| L[Evaluar fitness de nueva población]
L --> M[Ordenar por fitness]
M --> N[Guardar mejor fitness en historial]
N --> O{¿Mejora < epsilon?}
O -->|Sí| P
O -->|No| E
P --> Q[Fin]
De la teoría a la práctica
Dentro del diseño principal de los genéticos, hay una variedad muy grande de operadores. A lo largo de los años han ido surgiendo distintos diseños y evoluciones de los operadores básicos. Aquí implementaré los más sencillos.
La siguiente clase contiene los parámetros de inicialización del algoritmo. El parámetro fitness_func hace referencia a la función fitness. Esta es la función objetivo que vamos a maximizar. Veremos que de esta también depende la calidad de nuestra solución, pues hay múltiples formas de abordar la evaluación de un cromosoma. El resto de parámetros son evidentes: el tamaño de la población, número de genes de cada solución, probabilidad de mutación por gen, iteraciones máximas, mejora mínima por generación (cuando deja de mejorar un mínimo el algoritmo para), probabilidad de cruce, porcentaje de elitismo en función del tamaño de la población y una semilla (por reproducibilidad en experimentación).
La población se genera siguiendo una distribución discreta uniforme, pero esto es cuestión de diseño, podría utilizarse otra distribución.
class GA:
def __init__(
self,
fitness_func: Callable,
population_size: int,
num_genes: int,
mutation_rate: float,
max_iter: int,
epsilon: float,
crossover_rate: float = 0.8,
elitism_rate: float = 0.1,
seed: Optional[int] = None,
):
self.fitness_func = fitness_func
self.population_size = population_size
self.num_genes = num_genes
self.mutation_rate = mutation_rate
self.max_iter = max_iter
self.epsilon = epsilon
self.crossover_rate = crossover_rate
self.elitism_rate = elitism_rate
self.best_fitness_history = []
if seed is not None:
np.random.seed(seed)
random.seed(seed)
def initialize_population(self) -> np.ndarray:
self.population = np.random.randint(
low=0, high=2, size=(self.population_size, self.num_genes)
)
return self.population
El operador de cruce es sencillo. Este concretamente recibe el nombre de one-point crossover ya que se selecciona un punto al azar entre las dos soluciones padre.
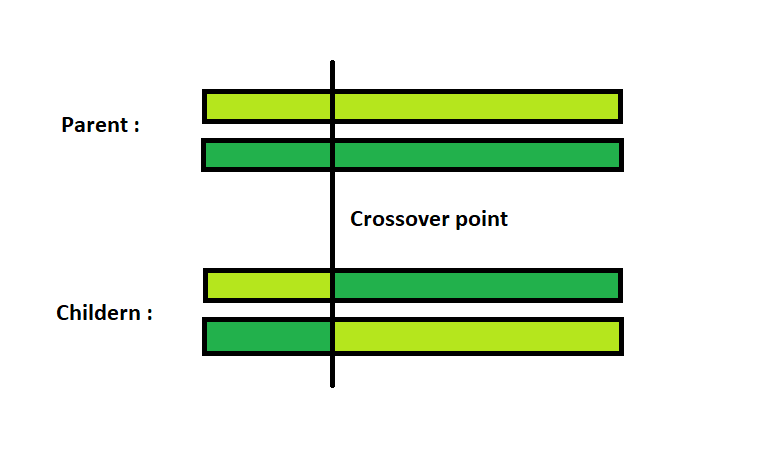
Dado ese punto de corte, se mezcla la parte izquierda de un padre con la parte derecha de otro y viceversa, generando en el proceso dos soluciones hijo.
def crossover(
self, x1: np.ndarray, x2: np.ndarray
) -> Tuple[np.ndarray, np.ndarray]:
if np.random.rand() > self.crossover_rate:
return x1.copy(), x2.copy()
point = np.random.randint(1, x1.size)
c1 = np.concatenate([x1[:point], x2[point:]])
c2 = np.concatenate([x2[:point], x1[point:]])
return c1, c2
El operador de mutación, en el caso de la mutación binaria, no tiene mucho misterio. Se recorre cada gen de un cromosoma, generando un número aleatorio por cada iteración. Con una probabilidad baja se realizará esa mutación, que consiste en un cambio del bit. Si era $0$ cambia a $1$ y viceversa. Esta probabilidad suele ser baja para evitar que el proceso se vuelva excesivamente aleatorio y se pierda la información genética acumulada por selección y cruce.
Este operador introduce aleatoriedad en el algoritmo, de forma que se favorece a la exploración del espacio de soluciones.
def mutate(self, x: np.ndarray) -> np.ndarray:
for i in range(x.size):
if np.random.rand() < self.mutation_rate:
x[i] = 1 - x[i]
return x
El operador de selección es uno de los componentes fundamentales de los algoritmos genéticos y se encarga de decidir qué individuos de la población pasan a reproducirse y, por tanto, a transmitir su información genética a la siguiente generación. Su funcionamiento se basa en el principio de la supervivencia del más apto, es decir, los que mejor evaluación tienen dada la función fitness. En este caso he implementado una ruleta, que es sencilla de programar y de entender. La probabilidad de selección de cada individuo es proporcional a su aptitud.
def roulette_wheel(self, scores: np.ndarray) -> np.ndarray:
if np.sum(scores) == 0 or np.count_nonzero(scores) < 2:
return np.random.choice(len(scores), 2, replace=False)
probs = scores / np.sum(scores)
return np.random.choice(len(scores), 2, replace=False, p=probs)
Finalmente, una vez se han explicado los operadores, queda la evolución generacional. Como he mencionado, se modifica la población completa generación tras generación siguiendo el siguiente bucle: Selección de padres, cruce de padres, mutación y reemplazo de la población. El elitismo es opcional, pero he optado por añadirlo ya que en mi experiencia no promueve una convergencia muy temprana si el número es bajo y mejora mucho la calidad de las soluciones.
def optimize(self) -> np.ndarray:
population = self.initialize_population()
scores = self.fitness_func(population)
idx = np.argsort(scores)[::-1]
population = population[idx]
scores = scores[idx]
prev_best = scores[0]
elite_size = int(self.elitism_rate * self.population_size)
for it in range(self.max_iter):
new_population = []
elites = population[:elite_size]
new_population.extend(elites)
while len(new_population) < self.population_size:
i1, i2 = self.roulette_wheel(scores)
p1, p2 = population[i1], population[i2]
c1, c2 = self.crossover(p1, p2)
c1 = self.mutate(c1)
c2 = self.mutate(c2)
new_population.append(c1)
if len(new_population) < self.population_size:
new_population.append(c2)
population = np.array(new_population)
scores = self.fitness_func(population)
idx = np.argsort(scores)[::-1]
population = population[idx]
scores = scores[idx]
best = scores[0]
self.best_fitness_history.append(best)
improvement = best - prev_best
if 0 < improvement < self.epsilon:
print(
f"Early stopping at iteration {it + 1}: improvement ({improvement:.6f}) < epsilon ({self.epsilon})"
)
break
prev_best = best
return population[0]
El problema de la mochila
Como problema de ejemplo para optimizar y visualizar el comportamiento de este algoritmo he escogido el problema de la mochila o Knapsack Problem, un clásico.
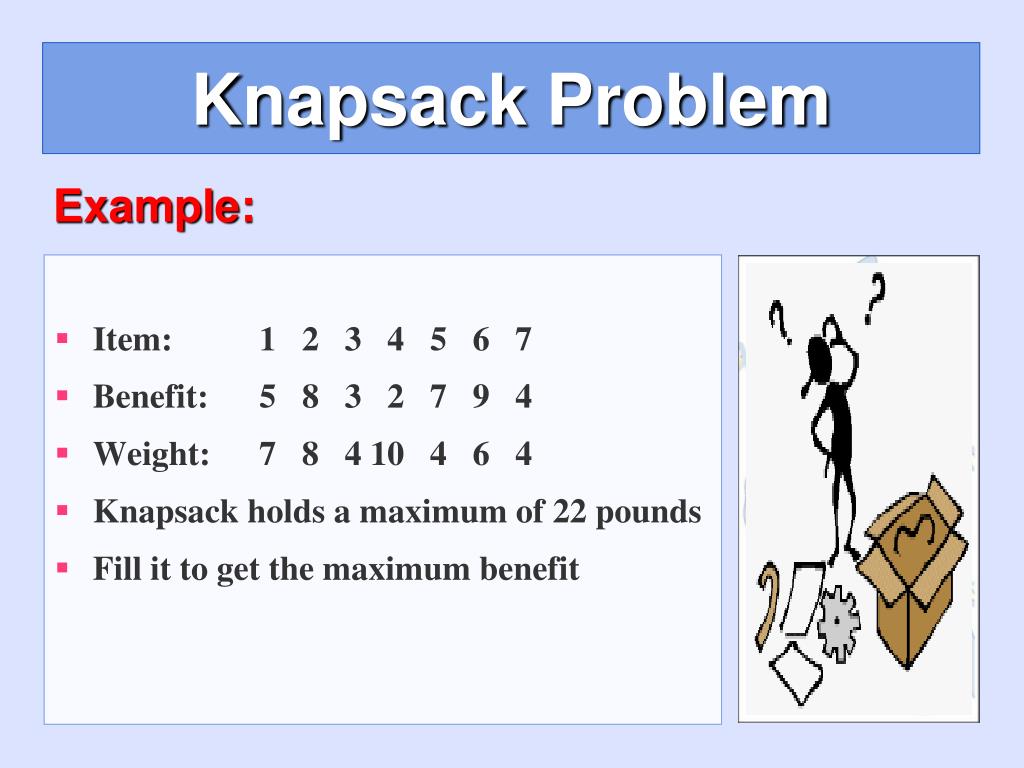
Este consiste en seleccionar, de entre un conjunto de objetos con un peso y un valor asociados, aquellos que deben introducirse en una mochila con capacidad limitada para maximizar el valor total sin exceder dicha capacidad.
Para poder trabajar en este problema con algoritmos genéticos, la codificación de las soluciones deberá tomar la forma de un vector binario, donde cada gen representa un objeto candidato a ser introducido en la mochila: el valor $1$ indica que el objeto es seleccionado y el valor $0$ que no lo es.
\[\mathbf{x} = (x_1, x_2, \dots, x_n), \quad x_i \in \{0,1\}, \quad x_i = \begin{cases} 1 & \text{si el objeto } i \text{ es seleccionado} \\ 0 & \text{en caso contrario} \end{cases}\] \[W(\mathbf{x}) = \sum_{i=1}^{n} w_i x_i \leq W_{\max}\] \[V(\mathbf{x}) = \sum_{i=1}^{n} v_i x_i\]En esta formulación, $\mathbf{x}$ es una solución candidata formada por $n$ objetos, $x_i$ indica la selección del objeto $i$, $w_i$ y $v_i$ representan respectivamente el peso y el valor del objeto $i$, $W(\mathbf{x})$ es el peso total de la solución, $W_{\max}$ la capacidad máxima de la mochila, y $V(\mathbf{x})$ el valor total de la solución, que se utiliza como función fitness.
Funciones de evaluación (fitness)
Vamos a probar a solucionar este problema con el algoritmo genético básico que he presentado previamente. Para ello, antes de todo, debemos escoger una función fitness. Aquí entran dos tipos de evaluaciones que podemos hacer sobre una solución. Si la solución se excede en carga, podemos penalizarla de forma drástica, añadiendo un score de $0$, por ejemplo, y dejando el valor total como score para aquellos cromosomas que no violen la restricción. Esto funciona, pero tiene problemas. Imaginemos que tenemos dos soluciones de igual valor. Una se excede por $4kg$ y otra se excede por $0.3kg$. La función de evaluación daría la misma puntuación a ambas soluciones, cuando claramente hay una peor que otra.
def fitness_knapsack_hard(
population: np.ndarray,
weights: np.ndarray,
values: np.ndarray,
max_capacity: int,
) -> np.ndarray:
total_weights = np.sum(population * weights, axis=1)
total_values = np.sum(population * values, axis=1)
total_values[total_weights > max_capacity] = 0.0
return total_values
Esto lo que le está diciendo al algoritmo es que debe darle la misma importancia a una que a otra. Podríamos estar sesgando la capacidad de exploración entre las ramificaciones de posibles soluciones hijas generadas a partir de la solución menos mala. También podría ocurrir que el algoritmo contenga una población de malas soluciones a las cuales no podría seguir evolucionando para intentar mejorar. Es una visión pesimista. La penalización binaria elimina la información sobre cómo de lejos está una solución de ser factible, reduciendo la capacidad del algoritmo para realizar mejoras graduales.
Una opción alternativa sería penalizar suavemente, teniendo en cuenta la magnitud de la violación. La función fitness_knapsack_soft evalúa cada individuo en base a su valor total. Si esa solución se excede en peso total del máximo permitido, se introduce una penalización gradual que crece de manera exponencial. El factor $\alpha$ controla si se aplica más o menos penalización.
def fitness_knapsack_soft(
population: np.ndarray,
weights: np.ndarray,
values: np.ndarray,
max_capacity: float,
alpha: float = 0.2,
) -> np.ndarray:
total_weights = np.sum(population * weights, axis=1)
total_values = np.sum(population * values, axis=1)
excess = np.maximum(0.0, total_weights - max_capacity)
penalty = np.exp(-alpha * excess)
return total_values * penalty
Resolución
Vamos a comparar el GA con varios tamaños de problema y distintas restricciones con la función de evaluación suave y la dura. Además vamos a compararlo con un algoritmo Greedy para analizar las diferencias en calidad de solución, tiempo de cómputo y cumplimiento de restricciones. El algoritmo Greedy es muy simple. Utiliza una heurística básica de ordenación y va escogiendo el mejor camino posible en cada paso hasta completar la solución final. Es muy rápido y, dependiendo de la heurística elegida, muy competente.
class Greedy:
def __init__(
self,
weights: np.ndarray,
values: np.ndarray,
max_capacity: float,
heuristic: str,
fitness_func: Callable,
):
self.weights = weights
self.values = values
self.max_capacity = max_capacity
self.fitness_func = fitness_func
self.heuristic = heuristic
self.best_fitness_history = []
def optimize(self) -> np.ndarray:
n = len(self.weights)
solution = np.zeros(n, dtype=int)
if self.heuristic == "h1":
ratios = self.values
order = np.argsort(-ratios)
elif self.heuristic == "h2":
ratios = self.weights
order = np.argsort(ratios)
else:
ratios = self.values / self.weights
order = np.argsort(-ratios)
remaining_capacity = self.max_capacity
best_fitness = float("-inf")
for i in order:
if self.weights[i] <= remaining_capacity:
solution[i] = 1
remaining_capacity -= self.weights[i]
current_fitness = self.fitness_func(solution.reshape(1, -1))[0]
if current_fitness > best_fitness:
best_fitness = current_fitness
self.best_fitness_history.append(best_fitness)
if not self.best_fitness_history:
self.best_fitness_history.append(
self.fitness_func(solution.reshape(1, -1))[0]
)
return solution
Para Greedy he definido tres heurísticas básicas. Ordenación de mejores objetos en función del valor, del peso y del valor relativo al peso.
| Heurística | Criterio | Idea | Razonamiento |
|---|---|---|---|
| h1 | Valor del ítem (↓) | Ítems más valiosos primero | Maximiza el beneficio absoluto |
| h2 | Peso del ítem (↑) | Ítems más ligeros primero | Maximiza el número de ítems |
| h3 | Valor / Peso (↓) | Ítems más eficientes | Maximiza la eficiencia valor–capacidad |
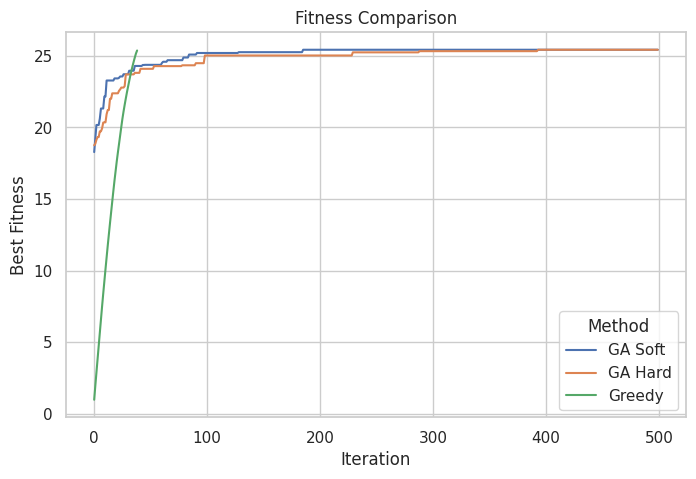
Para tamaños pequeños como $50$, algoritmo Greedy con la primera heurística y una restricción generosa del $40\%$ sobre el total de número de objetos, obtenemos resultados muy decentes:
=== SOFT CONSTRAINTS ===
Best fitness score: 25.419778639697903
Total weight: 19.959887918754212
Total value: 25.419778639697903
Max capacity: 20
=== HARD CONSTRAINTS ===
Best fitness score: 25.419778639697903
Total weight: 19.959887918754212
Total value: 25.419778639697903
Max capacity: 20
=== GREEDY ===
Best fitness score: 25.367928277332897
Total weight: 19.93102578451347
Total value: 25.367928277332897
Max capacity: 20
Todos los algoritmos muestran buenas soluciones, siendo los GAs ligeramente superiores. Aun así, los tres obtienen soluciones muy buenas. Las dos funciones de fitness funcionan igual de bien. También se observa que Greedy es mucho más rápido, ya que ha tardado en converger menos de $50$ iteraciones, mientras que los genéticos han necesitado más de $100$ para igualar el score. Aunque es algo obvio, el Greedy no realiza exploración, solo explota una heurística de forma voraz.
Si probamos a cambiar la restricción y hacerla más complicada (esta vez no se podrá superar el $5\%$ del total en peso) veremos algunos cambios en los resultados:
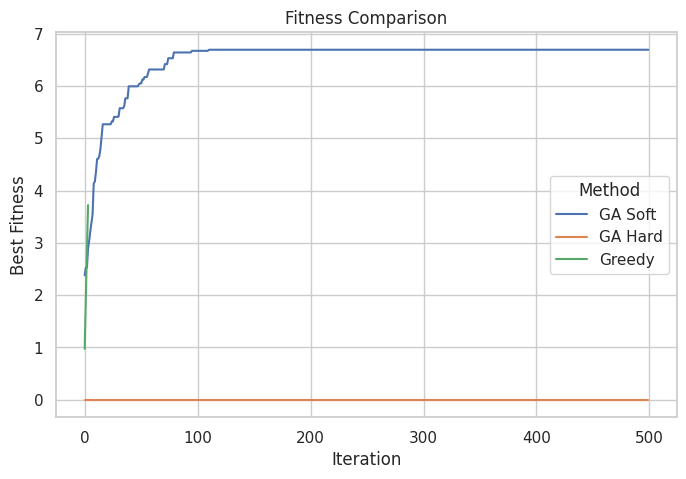
=== SOFT CONSTRAINTS ===
Best fitness score: 6.690651548303056
Total weight: 3.7789294493745977
Total value: 9.54957977253405
Max capacity: 2
=== HARD CONSTRAINTS ===
Best fitness score: 0.0
Total weight: 12.428228685377153
Total value: 13.08190249886287
Max capacity: 2
=== GREEDY ===
Best fitness score: 3.720164332689731
Total weight: 1.9952584283072372
Total value: 3.720164332689731
Max capacity: 2
Estos resultados ya son más interesantes. El algoritmo genético es igual en las dos comparaciones, pero la forma de evaluar es totalmente distinta. Con penalizaciones suaves o relativas, el algoritmo ha sido capaz de evaluar correctamente soluciones que eran a priori malas y las ha explorado y explotado inteligentemente obteniendo una solución final. En cambio las evaluaciones duras han destrozado la convergencia del genético y ha devuelto una solución sin refinar. De todas formas, el otro método no ha sido capaz de cumplir las restricciones impuestas, pasándose por $1.7$. Depende del contexto del problema, y esto es algo a evaluar dependiendo de las necesidades, esto podrá ser factible o inadmisible. La solución del Greedy, pese a no ser muy buena, cumple a rajatabla con el peso máximo permitido.
Probemos ahora con un tamaño más desafiante, un total de $200$ objetos y solo un $10\%$ de capacidad sobre el total permitido en la mochila:
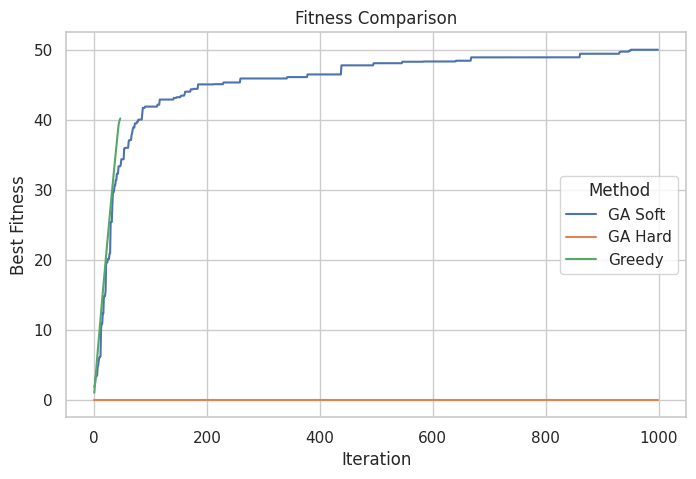
=== SOFT CONSTRAINTS ===
Best fitness score: 49.986377238685016
Total weight: 19.824506933869955
Total value: 49.986377238685016
Max capacity: 20
=== HARD CONSTRAINTS ===
Best fitness score: 0.0
Total weight: 56.058575444418665
Total value: 48.303356578426225
Max capacity: 20
=== GREEDY ===
Best fitness score: 40.175288587973824
Total weight: 19.997759251464615
Total value: 40.175288587973824
Max capacity: 20
La penalización dura sigue sin converger, mientras que el GA con fitness suave da los mejores resultados, con una convergencia suave y sin llegar a violar las restricciones impuestas. Los genéticos parecen una muy buena opción hasta ahora, pero probemos a cambiar una variable. Esta vez vamos a probar otra heurística en el algoritmo Greedy. La heurística número $3$, que ordena los objetos por el valor en relación al peso:
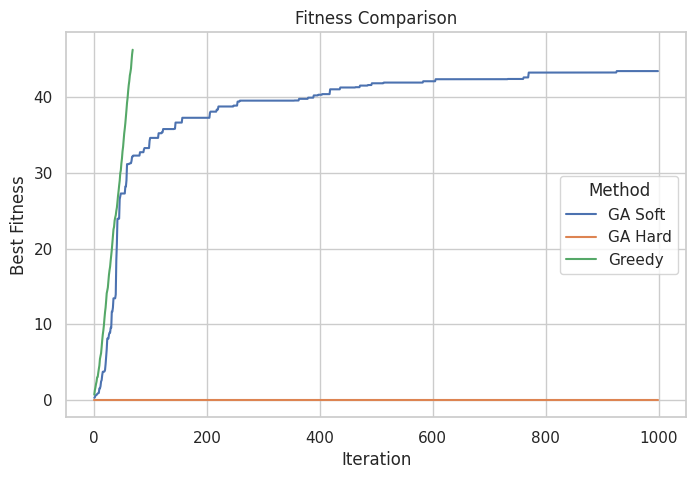
=== SOFT CONSTRAINTS ===
Best fitness score: 43.462952020478
Total weight: 19.97950402605357
Total value: 43.462952020478
Max capacity: 20
=== HARD CONSTRAINTS ===
Best fitness score: 0.0
Total weight: 51.83288833879617
Total value: 46.00902743825782
Max capacity: 20
=== GREEDY ===
Best fitness score: 46.28502186266642
Total weight: 19.94989976262729
Total value: 46.28502186266642
Max capacity: 20
El Greedy con la tercera heurística es no solo el más rápido, sino que es mejor, además de tener la garantía de no violar la restricción. Estos resultados ponen de manifiesto una idea clásica en optimización: una heurística sencilla, bien alineada con la estructura del problema, puede superar con facilidad a métodos mucho más complejos. En este caso, una ordenación simple basada en la eficiencia valor–peso permite al algoritmo Greedy encontrar soluciones de alta calidad de forma extremadamente rápida y sin violar las restricciones, incluso en escenarios más exigentes.
No obstante, esta ventaja depende fuertemente de la calidad de la heurística elegida. Cuando dicha heurística no captura adecuadamente la dinámica del problema, el rendimiento del enfoque voraz se degrada rápidamente. En contraste, los algoritmos genéticos muestran un comportamiento mucho más estable a lo largo de todos los escenarios analizados (sin ser esto un estudio riguroso ni de lejos). Con un diseño adecuado de la función de fitness, los GAs son capaces de explorar y explotar el espacio de soluciones de forma robusta, adaptándose a distintas restricciones y tamaños del problema sin colapsar.
Otras codificaciones
Finalmente, quería explicar que los algoritmos genéticos son en origen binarios, pero también aceptan otras codificaciones, como la continua, es decir, valores reales. Esto requiere de una adaptación sobre los operadores ya explicados para poder manejar este tipo de representación, pero la naturaleza del algoritmo es la misma. Este tipo de codificación abre la puerta a resolver problemas de optimización continua. He preparado una versión continua del GA, con ayuda de ChatGPT para crear unas animaciones, de forma que quede claro visualmente cómo converge la población hacia el máximo de la función definida. Las funciones que va a optimizar son las siguientes:
-
Sphere
\[f(x,y) = -\left(x^2 + y^2\right)\] -
Rastrigin
\[f(x,y) = -\left[ 2A + \left(x^2 - A\cos(2\pi x)\right) + \left(y^2 - A\cos(2\pi y)\right) \right], \quad A = 10\] -
Ackley
\[f(x,y) = -\left[ -20\, e^{-0.2\sqrt{0.5(x^2 + y^2)}} - e^{0.5(\cos(2\pi x) + \cos(2\pi y))} + e + 20 \right]\] -
Booth
\[f(x,y) = -\left[(x + 2y - 7)^2 + (2x + y - 5)^2\right]\]

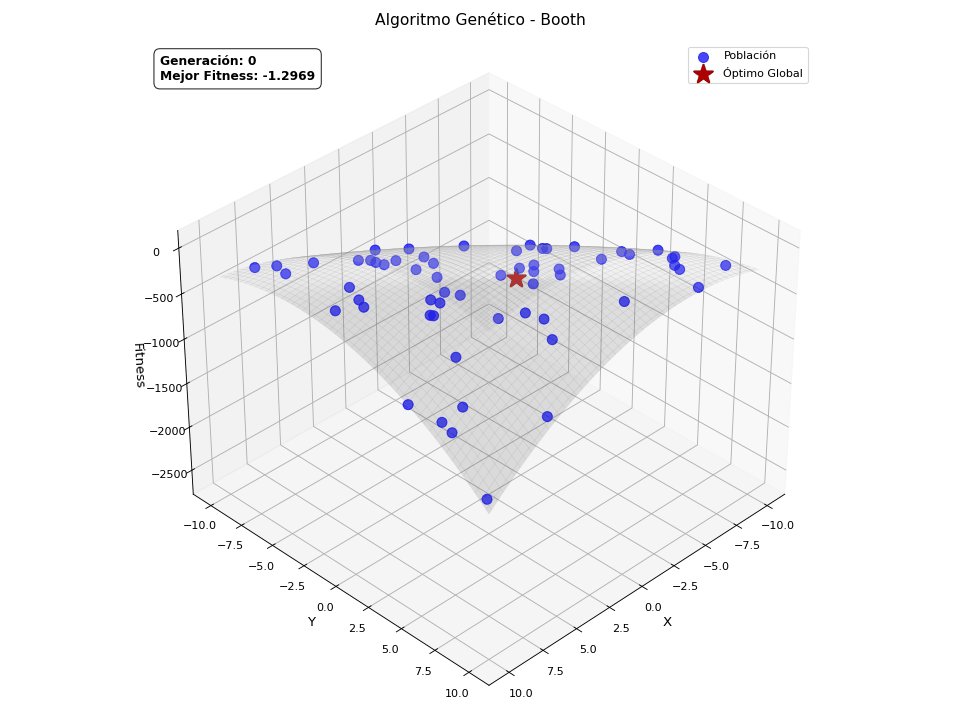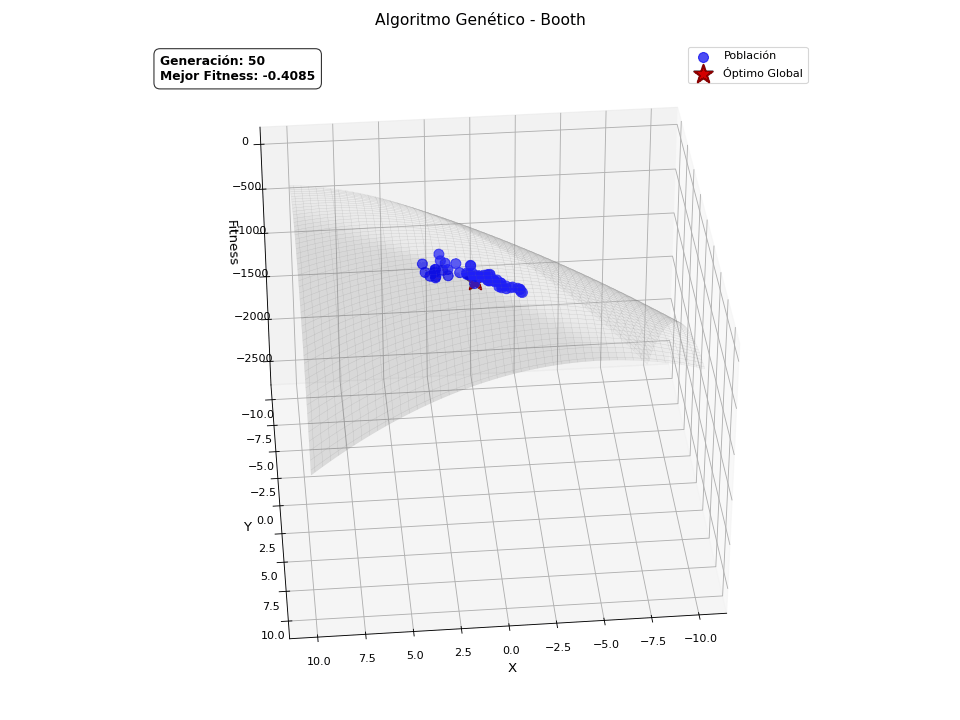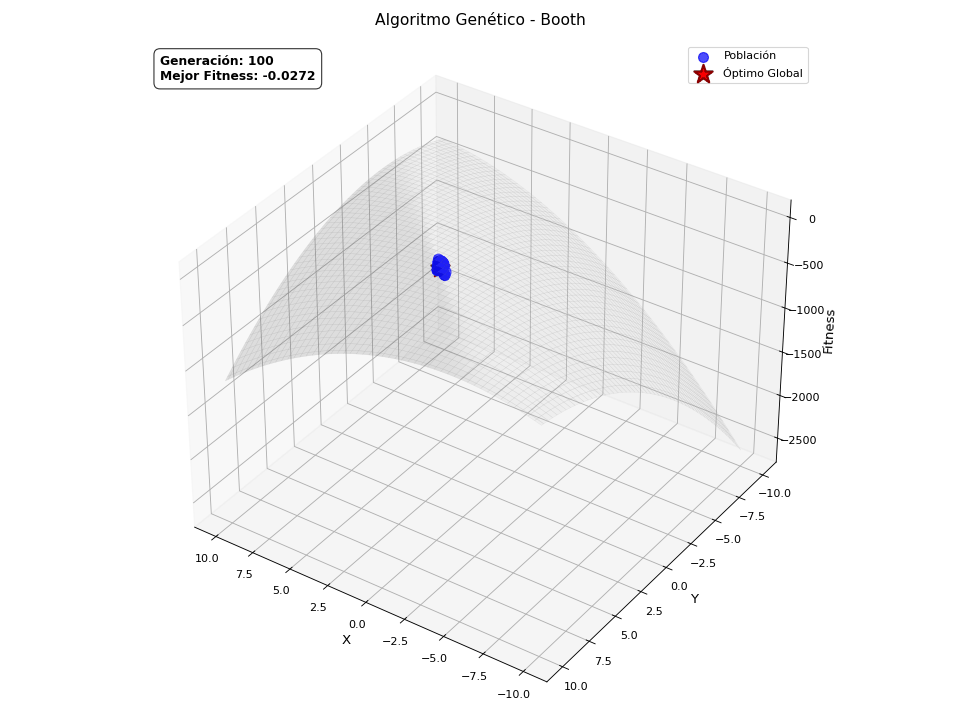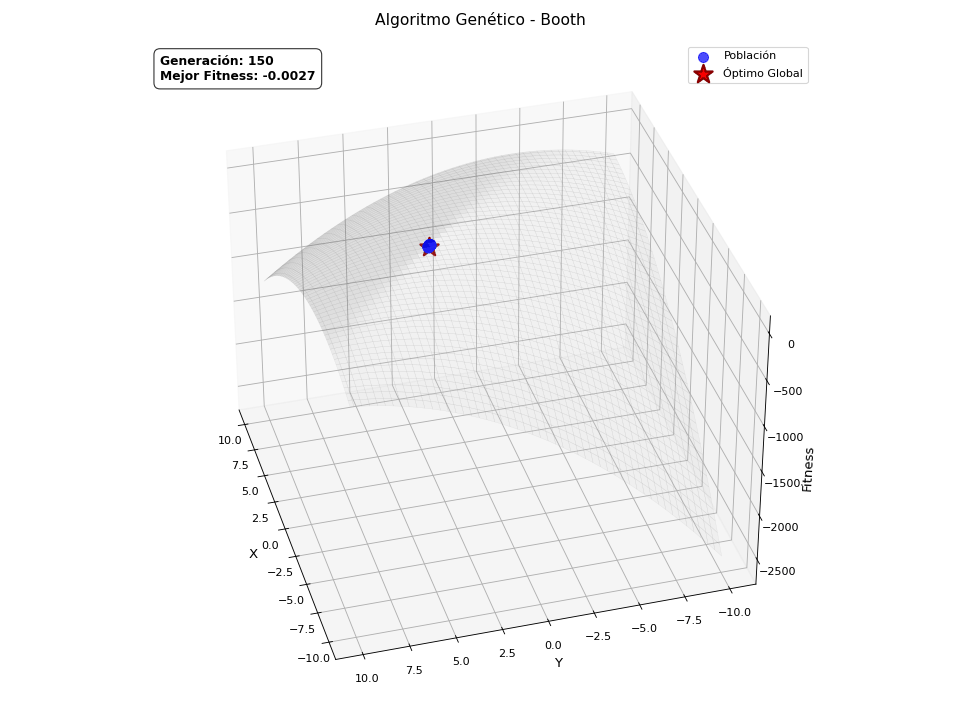
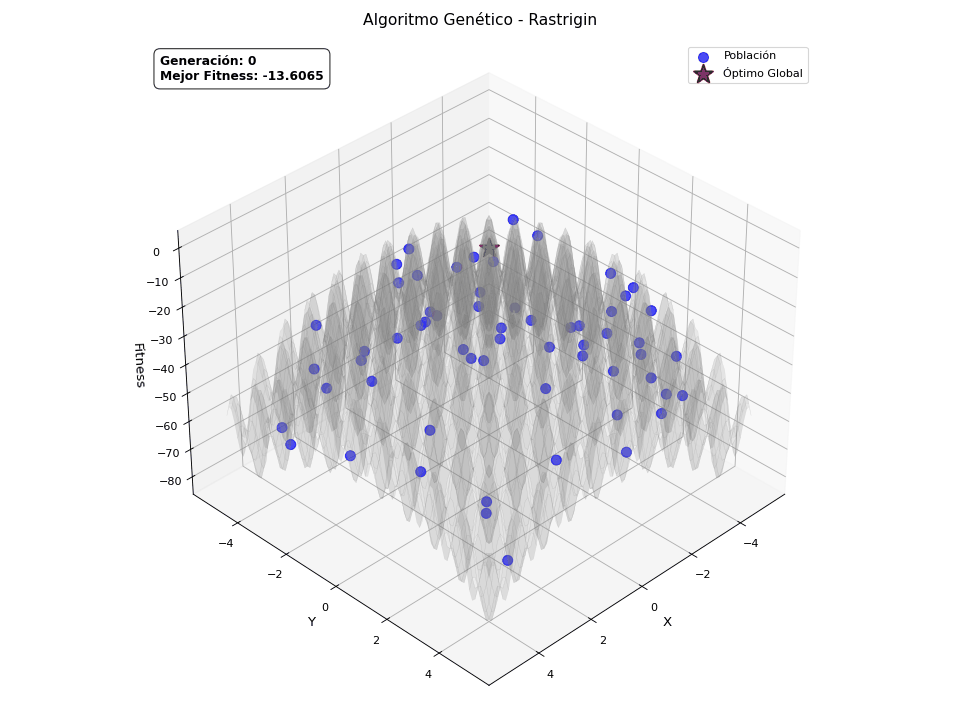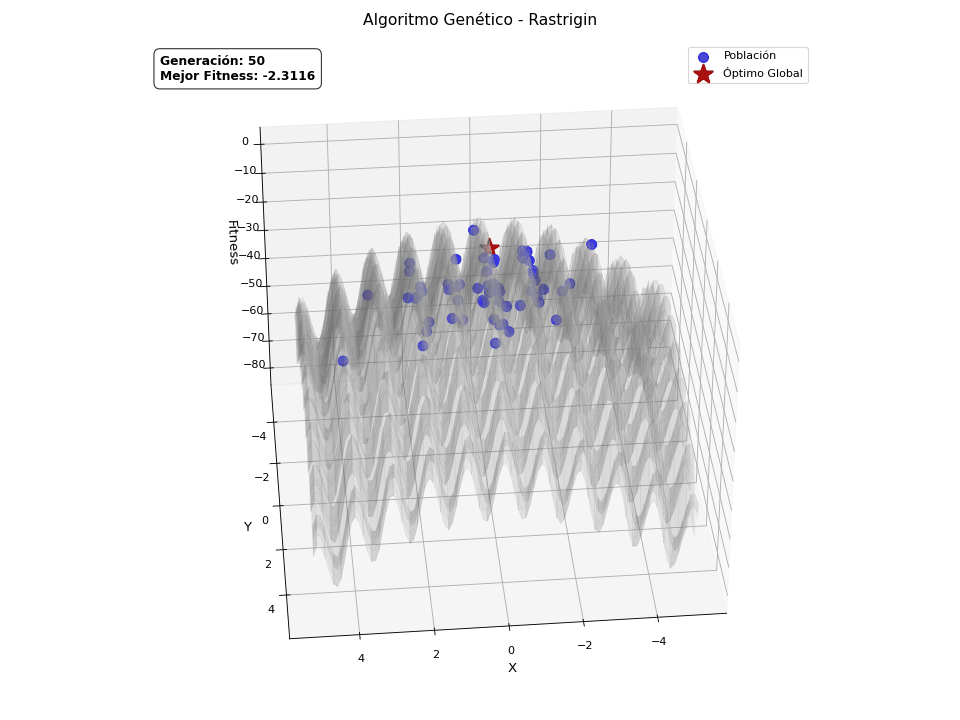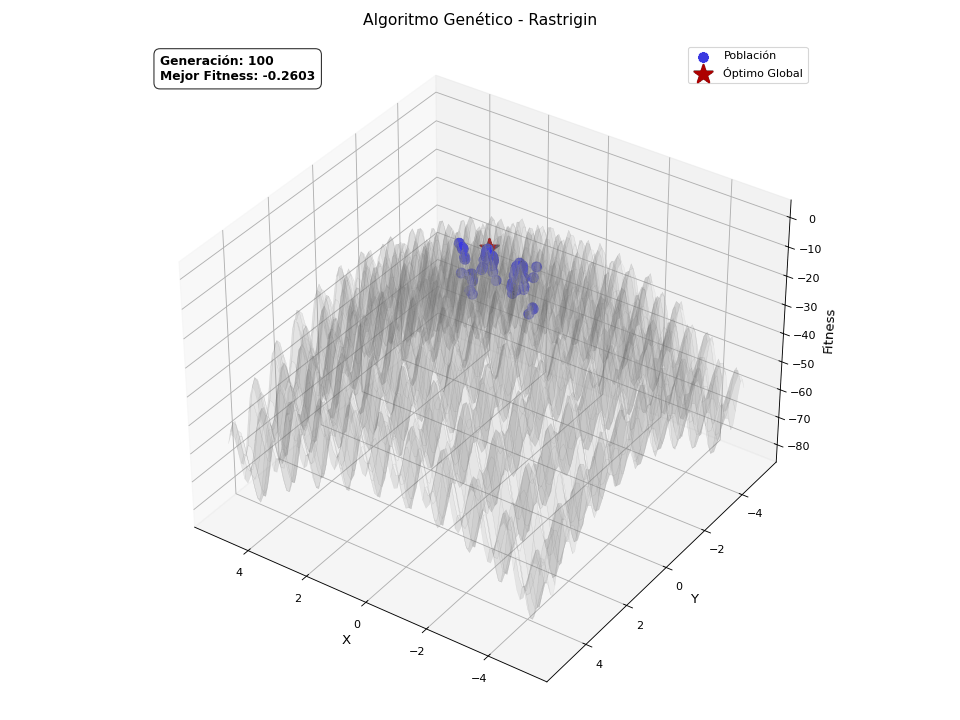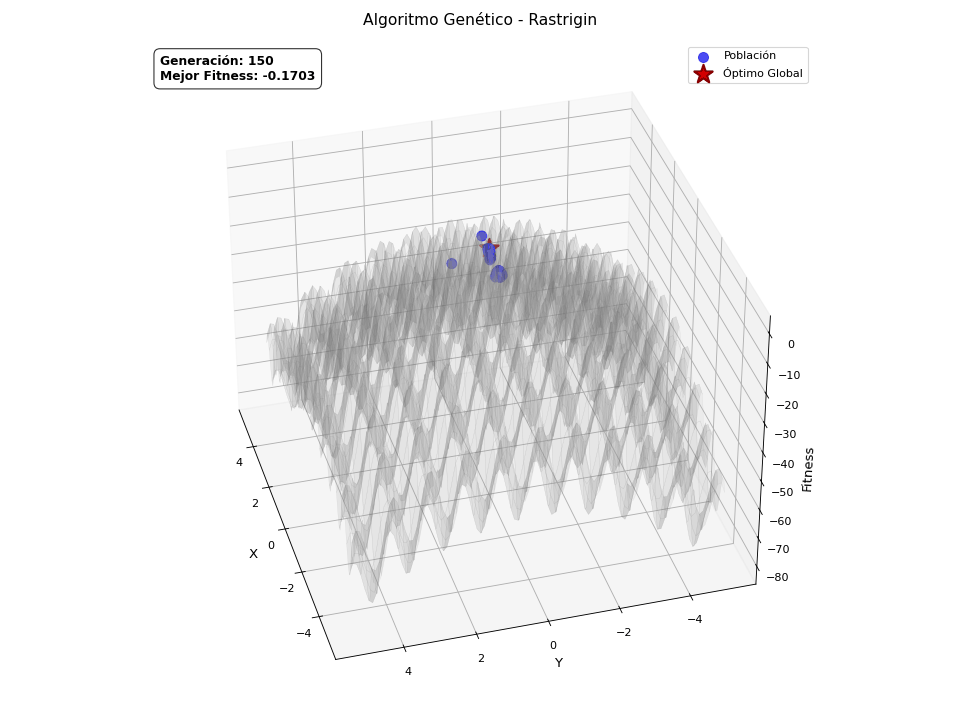
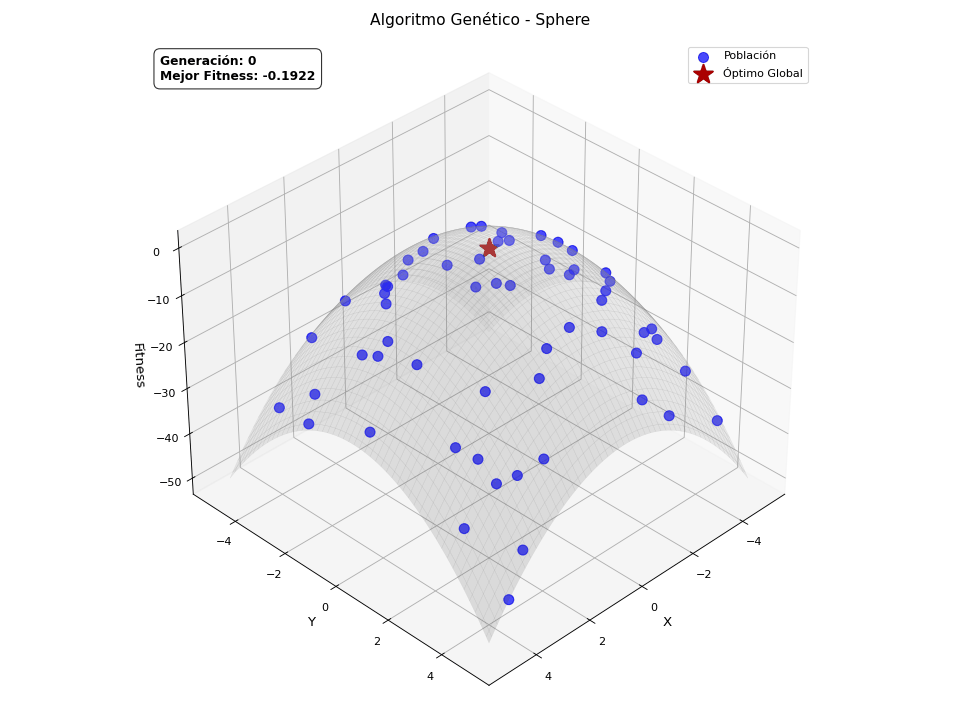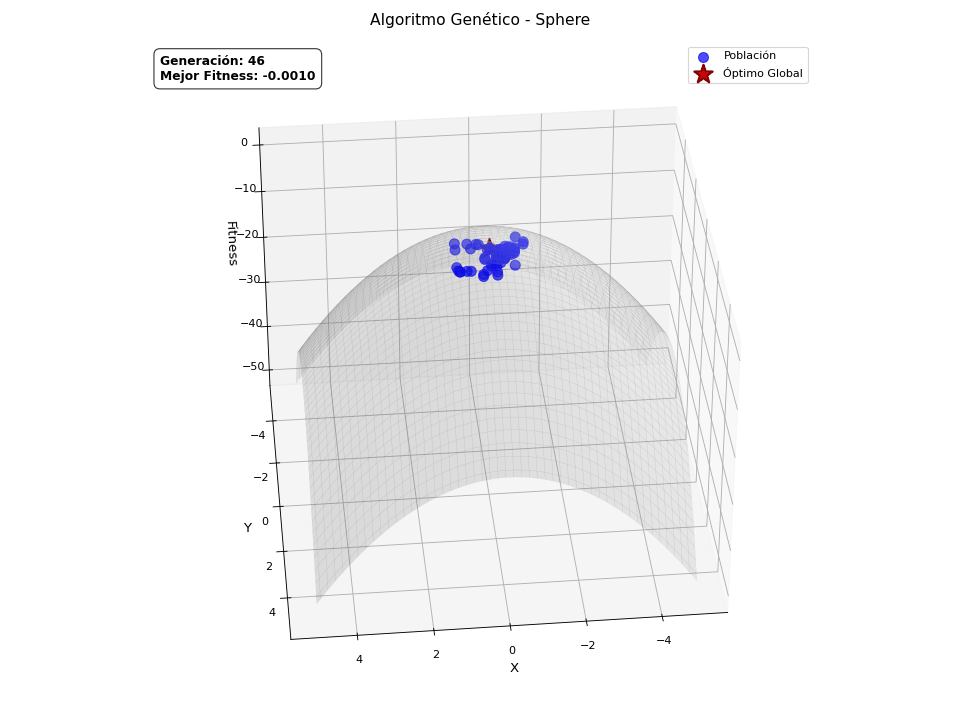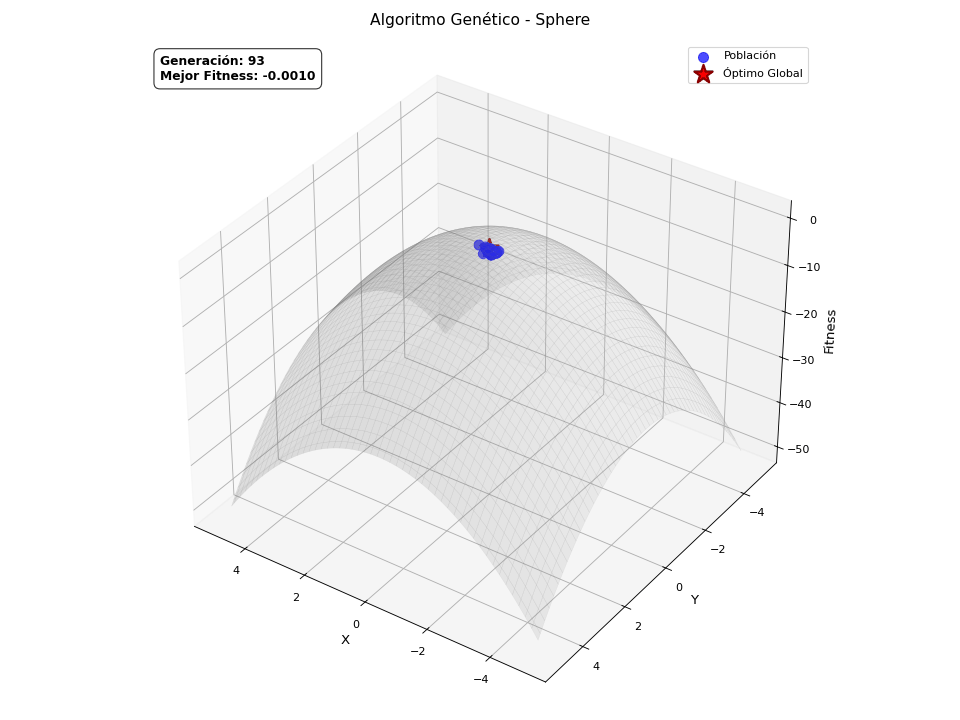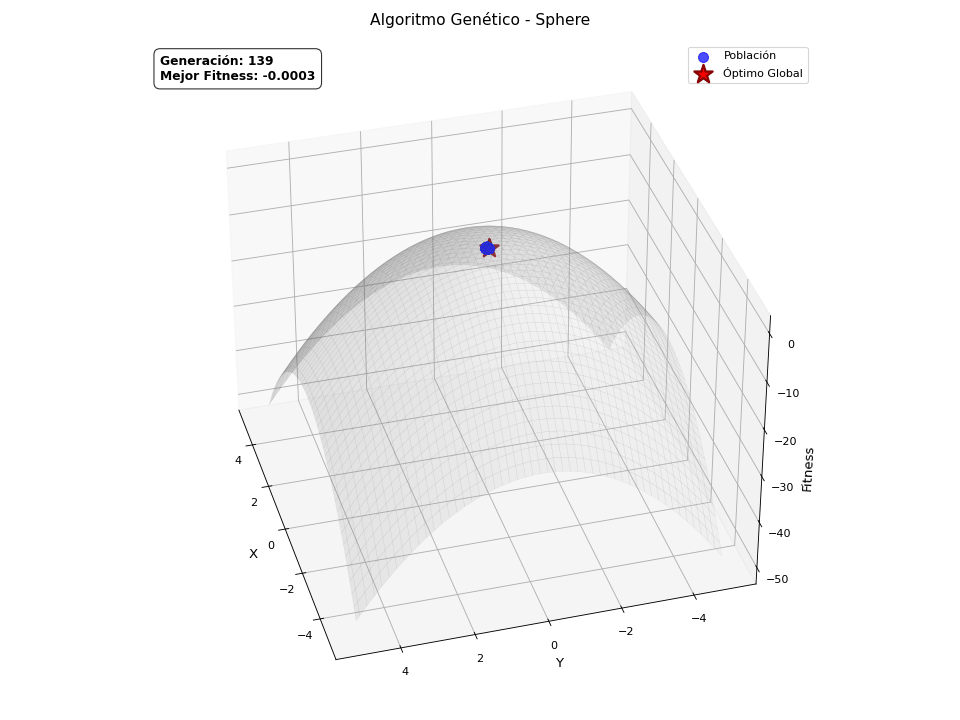
He de ser sincero, solo quería añadir estas animaciones porque molan.
Los algoritmos genéticos son uno de los muchos métodos metaheurísticos que existen. Desde luego no son los mejores, pero les tengo cariño y su diseño es inteligente a la par que sencillo. Es divertido programar GAs. Además, investigar en el camino las distintas decisiones de diseño que se pueden tomar, es enriquecedor.