¿Qué es la vectorización?
Como programador siempre he tenido en cuenta la eficiencia a la hora de crear sistemas. Los numeritos bajando, indicando poco tiempo de ejecución, nos producen cosquillas en el cerebro. Una forma de conseguir código más veloz es mediante la técnica de vectorización.
¿Qué es la vectorización entonces? Es un método por el cual aplicamos operaciones sobre un conjunto de elementos de forma simultánea, en vez de aplicarlas de una en una. Sencillo de entender y muy fácil de aplicar en Python con la librería de cálculo numérico NumPy.
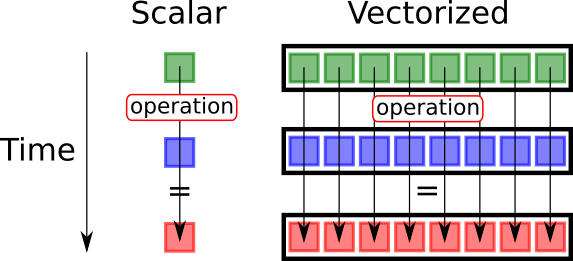
Sin embargo, no todos los problemas son vectorizables. Para que una operación pueda vectorizarse, los cálculos sobre cada elemento deben ser independientes entre sí, es decir, el resultado de un elemento no puede depender del resultado de otro. Esto es así porque las operaciones se ejecutan en paralelo. Si existiera dependencia entre los resultados, sería necesario coordinar la ejecución, introduciendo un overhead que reduciría, o incluso anularía, las ventajas en rendimiento.
También es necesario estructurar los datos en arrays o matrices, es decir, estructuras homogéneas. Las GPUs y CPUs están optimizadas para operar bajo estas estructuras. NumPy está programado para aprovechar estas optimizaciones.
Vectorización de un GA
Como ya vimos en mi anterior post cómo funcionan los algoritmos genéticos, podemos aprovechar el código secuencial en Python puro para introducir unas cuantas mejoras. Todos los operadores de ese código son perfectamente vectorizables. Al realizar el cambio, veremos una mejora muy sustancial, ya que los bucles en Python son inherentemente lentos.
Empecemos por el operador de mutación:
def mutate(self, x: np.ndarray) -> np.ndarray:
for i in range(x.size):
if np.random.rand() < self.mutation_rate:
x[i] = 1 - x[i]
return x
def mutate_vectorized(self, population: np.ndarray) -> np.ndarray:
mask = (
np.random.rand(population.shape[0], population.shape[1])
< self.mutation_rate
)
population[mask] = 1 - population[mask]
return population
En el primer código usé un for-loop en Python (extremadamente lento si el conjunto a iterar crece mucho) para ir mutando cada gen uno a uno. Además, se realiza la operación de generación de un número aleatorio individualmente.
En el segundo código creamos una máscara del tamaño de la población total. Véase que aquí operamos no sobre un individuo $x\in X$, sino sobre toda la población $X$. Si el número generado es menor a la probabilidad de mutación, entonces se aplica mutación. Después se aplica, de forma simultánea, la máscara sobre la operación para hacer el cambio de bit.
La diferencia es abismal. Asumamos unos $800$ genes por cromosoma con $50$ cromosomas y $200$ generaciones. En el primer código estaríamos iterando unas $800$ veces por cada individuo (unas $50\times 800=40.000$ iteraciones de un bucle for). Eso multiplicado por $200$ generaciones da unas $8.000.000$ iteraciones totales. En el segundo código se muta a la población de una generación de una sola vez. Pasamos de $8$ millones de iteraciones a unas $200$ operaciones vectoriales masivas.
def crossover(
self, x1: np.ndarray, x2: np.ndarray
) -> Tuple[np.ndarray, np.ndarray]:
if np.random.rand() > self.crossover_rate:
return x1.copy(), x2.copy()
point = np.random.randint(1, x1.size)
c1 = np.concatenate([x1[:point], x2[point:]])
c2 = np.concatenate([x2[:point], x1[point:]])
return c1, c2
def crossover_vectorized(
self, population: np.ndarray, indices: np.ndarray
) -> np.ndarray:
n_pairs = len(indices) // 2
parents1 = population[indices[::2]]
parents2 = population[indices[1::2]]
offspring = np.empty((n_pairs * 2, self.num_genes), dtype=population.dtype)
crossover_mask = np.random.rand(n_pairs) <= self.crossover_rate
crossover_points = np.random.randint(1, self.num_genes, size=n_pairs)
gene_indices = np.arange(self.num_genes)
masks = gene_indices[None, :] < crossover_points[:, None]
offspring[::2] = np.where(masks, parents1, parents2)
offspring[1::2] = np.where(masks, parents2, parents1)
no_crossover_mask = ~crossover_mask
offspring[::2][no_crossover_mask] = parents1[no_crossover_mask]
offspring[1::2][no_crossover_mask] = parents2[no_crossover_mask]
return offspring[: self.population_size]
El operador de cruce original trabaja a nivel de un solo par de individuos. Para cada pareja de padres, primero decide si se aplica o no el cruce en función de una probabilidad. En caso afirmativo, selecciona un punto de cruce y construye dos descendientes concatenando segmentos de los cromosomas parentales. Este proceso es conceptualmente simple y fácil de entender, pero requiere un bucle externo que itere sobre todos los pares de la población, lo que introduce un coste significativo cuando el tamaño poblacional o el número de genes es elevado.
La operación propiamente vectorizada aquí es el cruce de genes de todos los pares a la vez, sin bucles explícitos en Python. La operación np.where aplica la selección elemento a elemento sobre toda la matriz en una sola llamada.
Finalmente, los pares que no debían cruzarse se gestionan sobrescribiendo los descendientes generados con copias directas de los padres originales. Esta etapa mantiene la semántica del operador de cruce clásico, pero sigue utilizando indexación booleana vectorizada. El resultado es un algoritmo que conserva exactamente el mismo comportamiento genético que la versión iterativa, pero con una implementación más adecuada para grandes poblaciones.
La función principal optimize se simplifica bastante. Quedaría así:
def optimize(self) -> np.ndarray:
population = self.initialize_population()
scores = self.fitness_func(population)
idx = np.argsort(scores)[::-1]
population = population[idx]
scores = scores[idx]
prev_best = scores[0]
elite_size = int(self.elitism_rate * self.population_size)
for it in range(self.max_iter):
if np.sum(scores) == 0 or np.count_nonzero(scores) < 2:
parent_indices = np.random.choice(
len(scores), self.population_size, replace=True
)
else:
probs = scores / np.sum(scores)
parent_indices = np.random.choice(
len(scores), self.population_size, replace=True, p=probs
)
offspring = self.crossover_vectorized(population, parent_indices)
offspring = self.mutate_vectorized(offspring)
elites = population[:elite_size]
offspring = offspring[: self.population_size - elite_size]
population = np.vstack([elites, offspring])
scores = self.fitness_func(population)
idx = np.argsort(scores)[::-1]
population = population[idx]
scores = scores[idx]
best = scores[0]
self.best_fitness_history.append(best)
improvement = best - prev_best
if 0 < improvement < self.epsilon:
break
prev_best = best
return population[0]
Comprobación de la mejora
Ahora, ya tendríamos un GA mucho más optimizado. Los operadores principales se han reescrito de forma que aprovechen las ventajas de la vectorización. Ahora son capaces de aplicar operaciones masivas sobre toda la población, en vez de utilizar bucles de Python, los cuales son extremadamente lentos.
Para probar la eficacia de la vectorización, he programado un ejemplo en el que se lanzarán $5$ experimentos. Cada experimento tiene un tamaño de problema mayor que el anterior, en este caso el problema de la mochila, el cual ya expliqué en el post sobre genéticos. En cada experimento se hacen $5$ runs para minimizar el efecto de la aleatoriedad.
Antes de todo, definamos el speed-up:
\[speed\_up=\frac{T_{secuencial}}{T_{vectorizado}}\]Es decir, es una métrica que mide cuántas veces es una versión más rápida que la otra. Un speed-up de $\times 2$ significa que la versión vectorizada tarda la mitad de tiempo.
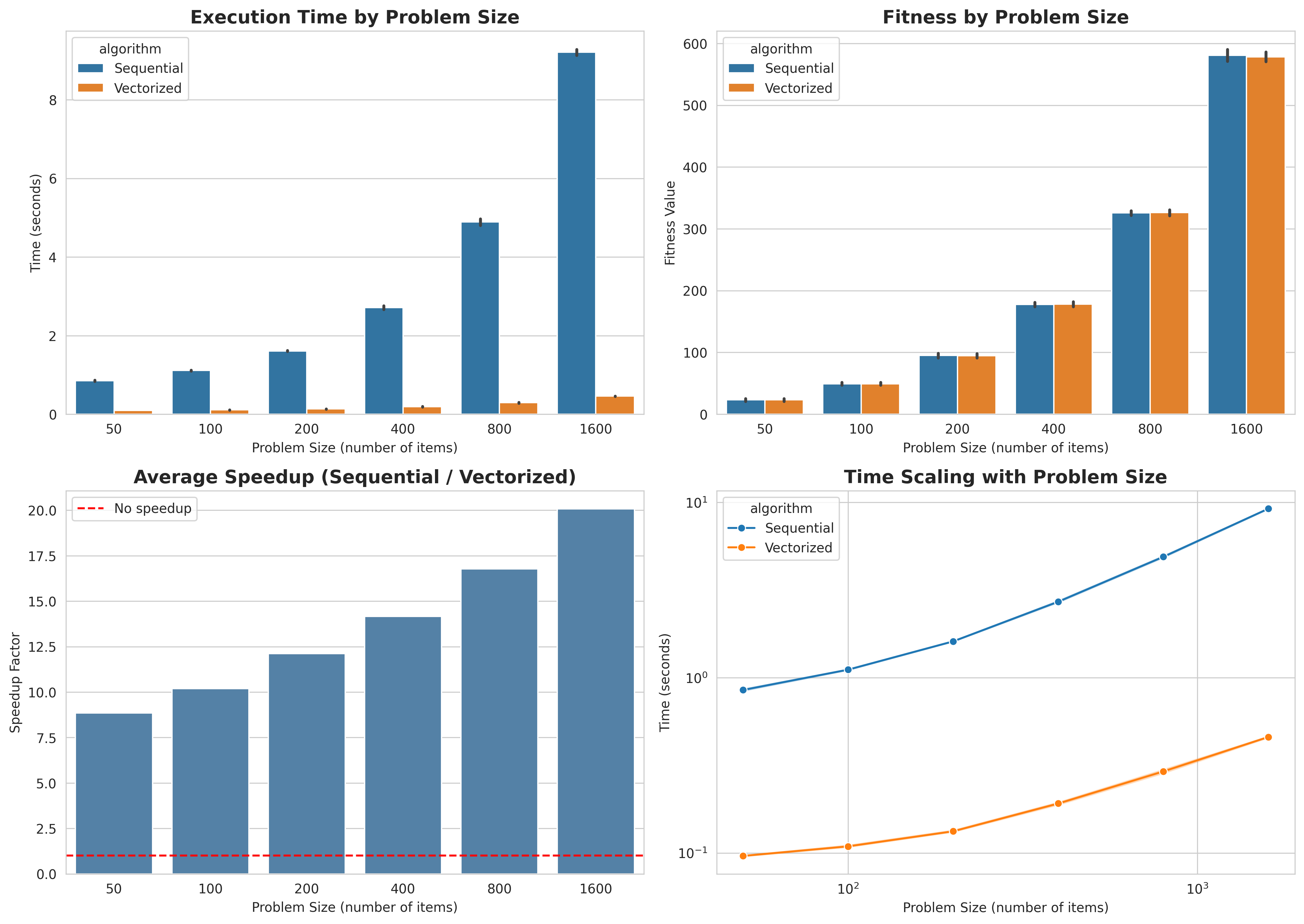
En el gráfico se muestra el tiempo de ejecución en términos absolutos, siendo el vectorizado mucho mejor. El valor del fitness de las mejores soluciones son prácticamente iguales. Irrelevante, pero quería mostrarlo, ya que debe quedar claro que la función y capacidad del GA queda inalterada. El speed-up crece según aumenta el tamaño del problema, es decir, es más eficiente que el secuencial según crece el problema, pero esto solo ocurre en el número limitado de ejecuciones que hemos hecho. Analicemos como escalan ambos algoritmos.
Ambas versiones muestran una tendencia de crecimiento similar en escala logarítmica, lo que indica que comparten el mismo orden de complejidad. Sin embargo, el algoritmo vectorizado presenta una constante multiplicativa mucho menor, lo que se traduce en una mejora sustancial del tiempo de ejecución para cualquier tamaño de problema.
¿El resumen de todo esto? El speed-up probablemente tope con un límite según crece el problema, pero aún así será unas $\approx\times 2$ veces mejor que el secuencial. Si aumentásemos el tamaño del problema más veces, veríamos como la tendencia alcista de la eficiencia se suaviza.
El cambio de mentalidad
La moraleja es sencilla: la vectorización es una herramienta sencilla de aplicar y muy beneficiosa.
Menos bucles en Python, más operaciones en bloque, y un GA que escala mucho mejor sin cambiar su comportamiento genético. La idea clave es cambiar el chip: dejar de pensar en individuos sueltos y empezar a pensar en poblaciones completas. Al menos en mi experiencia, una vez haces ese click mental, empiezas a ver oportunidades de vectorización por todas partes.