El teorema del límite central
El teorema del límite central es una idea clave y muy conveniente en la estadística. Este concepto nos permite extrapolar información a partir de muestras bien seleccionadas sobre la población. Lo que nos dice este teorema es que, si obtenemos distintas muestras para un tamaño muestral suficientemente grande y posteriormente hacemos la media de cada muestra, dichas medias se aproximan a una distribución normal. ¿Qué significa eso? Vayamos por partes. En estadística, una muestra no es más que un subconjunto aleatorio de una población. Una población es un conjunto que contiene todos los individuos, elementos u observaciones posibles. Es decir, imaginemos que queremos obtener la media del sueldo en España para todos los trabajadores en activo.
En este caso, la población recogería a todos los trabajadores de España en activo. Recoger datos de todos ellos resultaría casi imposible y muy costoso en la práctica, por eso es mejor seleccionar aleatoriamente a varios individuos que encajen en este perfil para obtener la información que buscamos. Estos individuos formarían las muestras. Supongamos que tomamos una muestra aleatoria de $50$ trabajadores de toda España. Es posible que, por azar, nuestra muestra incluya más gente de zonas con sueldos altos o bajos, y la media resultante se aleje de la media real. Esa variabilidad es natural. Cada muestra dará un resultado ligeramente distinto. Lo que nos dice el teorema del límite central es cómo se distribuyen esas medias si pudiéramos repetir el muestreo muchas veces. Si nos vamos a la Costa del Sol, seguramente estemos valorando muy positivamente lo que ganan en promedio los españoles. Lo mismo ocurriría en un barrio pobre, donde ahora estaríamos sesgando la métrica hacia abajo.
Es aquí donde el teorema del límite central hace su magia. Si cogemos las muestras y promediamos sus valores, vemos que la distribución estadística que siguen las medias de las muestras es similar a una normal. Cada media muestral es ya un estimador insesgado de la media poblacional. El teorema del límite central nos dice cómo se distribuye ese estimador cuando repetimos el experimento muchas veces. Estaríamos obteniendo información sobre el conjunto completo, pero sin haber tenido que recolectar datos de todos los trabajadores. Pero ojo, es importante que el tamaño muestral (el número de trabajadores a los que preguntamos cada vez) sea suficientemente alto. Depende de lo complicada que sea la distribución de la población, quizá sea necesario un número más alto o más bajo, pero generalmente cuanto más, mejor. De hecho, típicamente se establece el número $30$ como el límite mínimo para que la distribución de las medias empiece a asemejarse a una normal. Pero como he explicado, esto no siempre es así, depende.
Esto nos permite además tener información sobre la incertidumbre, es decir, sobre el error que podríamos estar cometiendo al estimar la media poblacional. Gracias a estar siguiendo una distribución normal, nos podemos someter a sus reglas. Y conocemos muy bien sus reglas.
Ejemplo práctico
Simulemos rápidamente en Python el teorema del límite central. La distribución de la población en este caso es uniforme discreta, es decir, vamos a generar números enteros, concretamente entre el $0$ y el $9$, y cada uno de ellos tiene las mismas probabilidades de salir en cada muestra que obtengamos. El código con NumPy quedaría tal que así:
np.mean(np.random.randint(0, 10, sample_size))
Lo que estamos haciendo es muestrear números enteros de una distribución uniforme. El parámetro sample_size indica cuantas observaciones tiene la muestra.
Ahora vamos a repetir este muestreo tantas veces como queramos. En este caso un total de $10000$ veces. Si cogemos la media de cada muestra y construimos un vector con ellas, podemos crear un histograma para ver que distribución sigue:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
def main():
n_samples = 10000
sample_size = 1
sample_means = [
np.mean(np.random.randint(0, 10, sample_size))
for _ in range(n_samples)
]
sns.histplot(sample_means, bins=50, kde=True)
plt.title("Central Limit Theorem: Distribution of Sample Means")
plt.xlabel("Sample Mean")
plt.ylabel("Frequency")
plt.savefig(f"scripts/central_limit_theorem/clt_{sample_size}.png")
plt.close()
if __name__ == "__main__":
main()
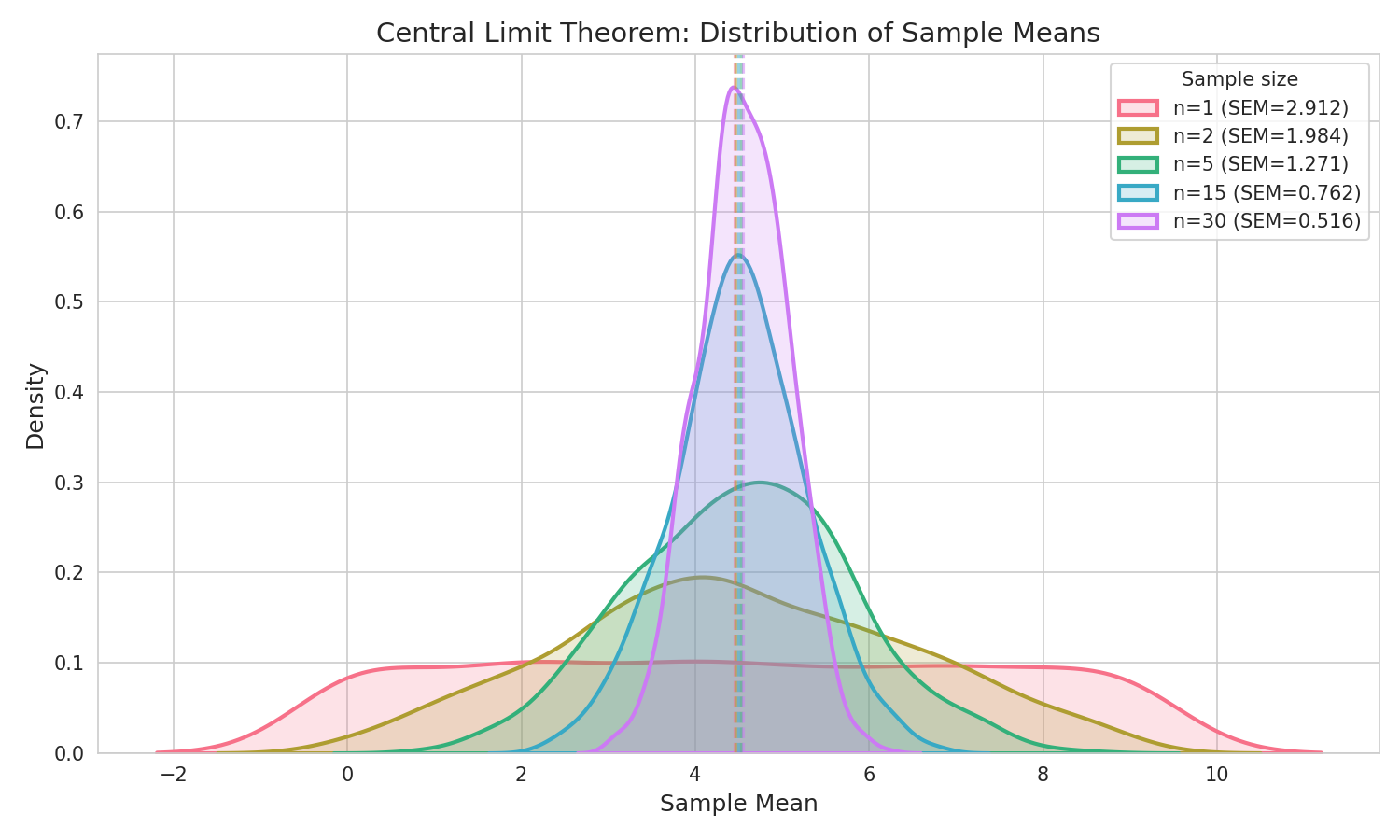
En la siguiente imagen podemos ver, de izquierda a derecha y de arriba a abajo, las distribuciones resultantes. Con solo una observación por muestra, obtenemos la distribución original, en este caso la uniforme. La media de cada muestra es el propio valor, por tanto, cada entero ha salido casi las mismas veces que el resto de enteros. Con un tamaño muestral de dos observaciones ya empieza a tomar una forma acampanada. Si se sigue aumentando el tamaño muestral, la media muestral, que al final es una aproximación a la media poblacional o valor esperado, será cada vez más fiel.
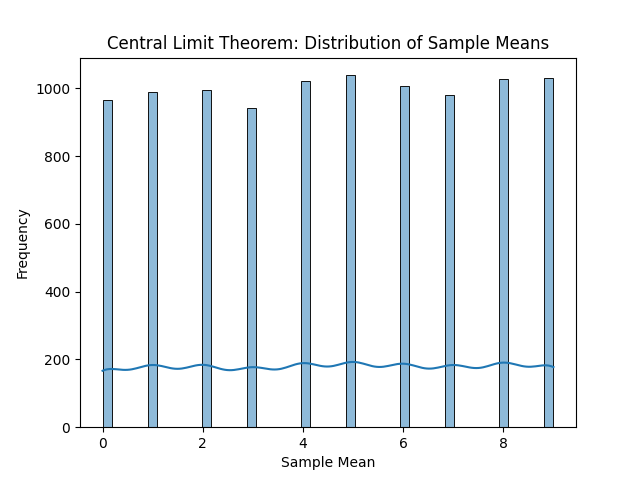
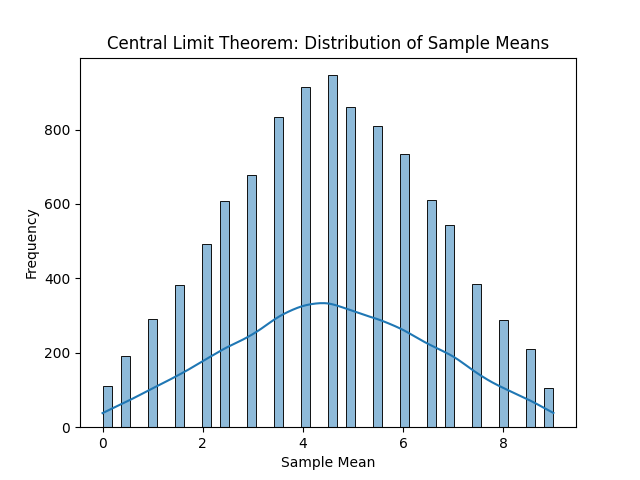
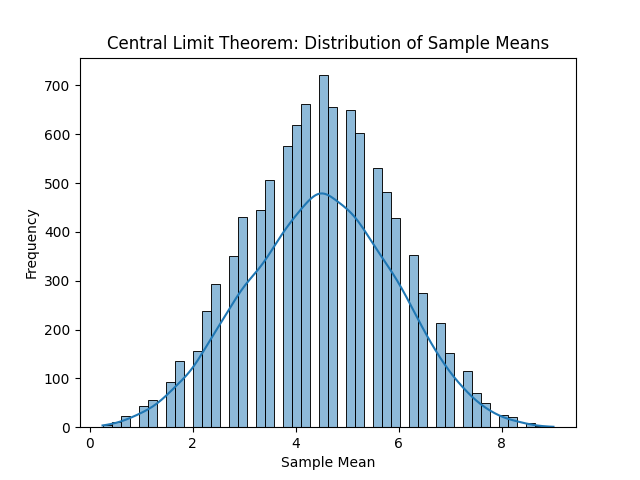
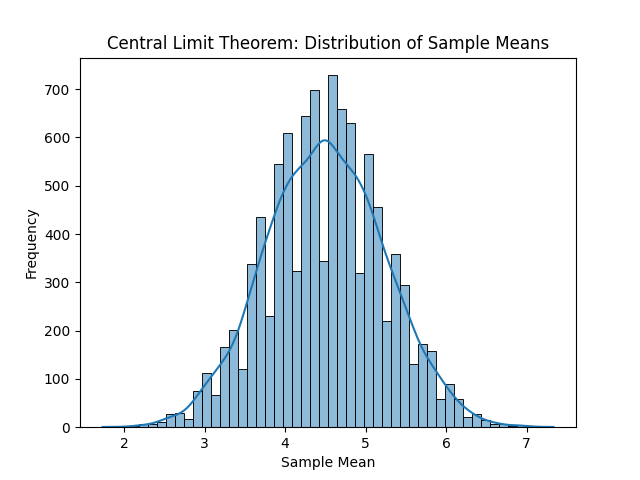
Por supuesto podemos seguir incrementando el tamaño muestral, pero concretamente para la distribución original uniforme no tiene mucho sentido. Es una distribución sencilla, por lo que con unas muestras relativamente pequeñas es suficiente para observar la campana de Gauss.
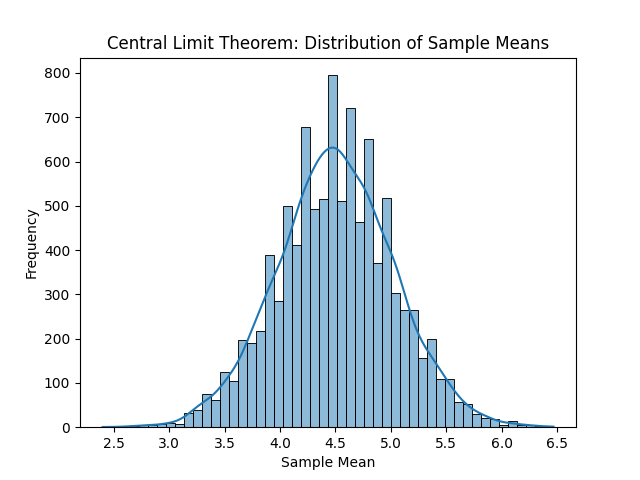
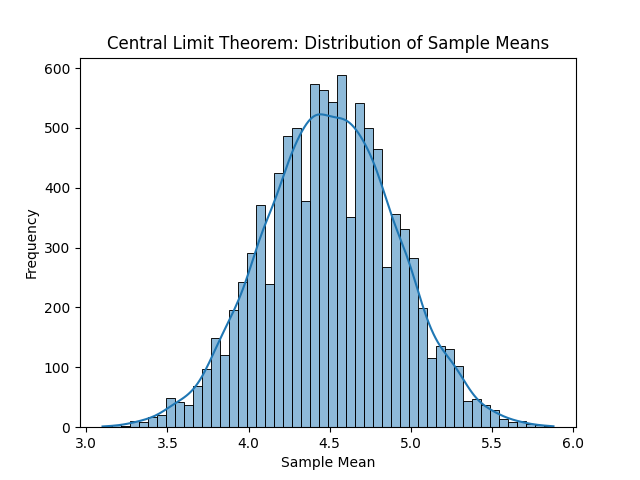
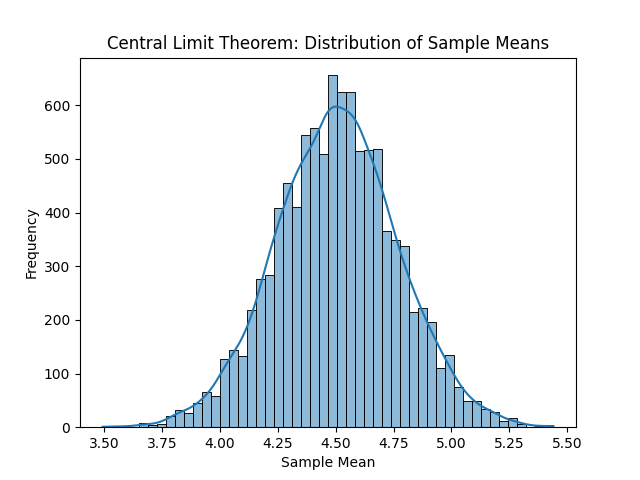
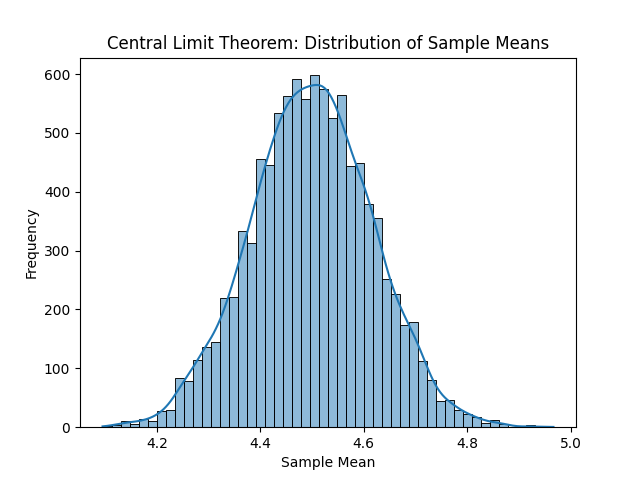
¿Qué podemos inferir a partir de todo esto?
La verdadera potencia del teorema del límite central no está solo en que “aparezca una campana”, sino en todo lo que nos permite inferir a partir de ella. Una vez sabemos que la media muestral sigue (aproximadamente) una distribución normal, podemos empezar a cuantificar la incertidumbre de nuestras estimaciones.
En primer lugar, podemos hablar del error estándar de la media, que no es más que la desviación típica de la distribución de las medias muestrales. Este valor nos dice cuánto esperamos que varíe la media muestral alrededor de la media poblacional real. Matemáticamente, este error estándar se define como:
\[\frac{\sigma}{\sqrt{n}}\]donde \(\sigma\) es la desviación típica de la población y \(n\) el tamaño muestral. Aquí aparece una idea clave: a mayor tamaño muestral, menor incertidumbre. No porque la media “sea mejor” por arte de magia, sino porque estamos reduciendo la variabilidad de nuestro estimador.
Gracias a esto, podemos construir intervalos de confianza. Por ejemplo, un intervalo de confianza del $95\%$ nos indica que, si repitiéramos el proceso de muestreo muchas veces, el $95\%$ de los intervalos construidos contendrían la media poblacional verdadera. Intuitivamente, no estamos diciendo que la media sea exactamente un número concreto, sino que estamos bastante seguros de que se encuentra en cierto intervalo alrededor de nuestra estimación.
Por último, todo esto nos recuerda algo importante: no solo importa el valor que estimamos, sino también el error que cometemos al estimarlo. El teorema del límite central nos da un marco matemático sólido para medir esa incertidumbre y tomar decisiones informadas, incluso cuando no conocemos la distribución real de la población.
Este truquito estadístico se usa en multitud de ámbitos y métodos, algunos de ellos muy relacionados con el machine learning, como la fórmula del error cuadrático medio o MSE. En un futuro post hablaré de ello y cómo su fórmula se puede explicar y entender mejor gracias a este concepto estadístico.