El origen del aprendizaje
El aprendizaje profundo o deep learning en inglés, es una disciplina que ha traído multitud de avances en todos los aspectos de nuestras vidas. Puede que no lo sepamos y lo demos por hecho, pero TODO hoy en día tiene “IA”. Digo inteligencia artificial, porque es una palabra casi desvirtuada y usada para todo desde que redes neuronales complejísimas como GPT llegaron a nuestras vidas hace unos pocos años. Pero la IA lleva con nosotros desde siempre. Cuando quieres desbloquear el móvil con la cara, se usa IA. Cuando traducimos de un idioma a otro con DeepL o Google Translator, se usa IA. Cuando se extrae texto a partir de una imagen, se usa IA. Cuando detectan lo que estás diciendo a partir de un audio, se usa IA.
La inteligencia artificial es un conjunto muy grande, como expliqué en mi primer post. Todo lo que he mencionado anteriormente, e incluso casos mucho más simples, usan redes neuronales, que pertenecen al área del aprendizaje profundo. El aprendizaje profundo es a su vez un subconjunto del aprendizaje automático, con la diferencia de que está totalmente especializado en redes neuronales profundas, en su arquitectura y su optimización.
El origen del aprendizaje, de la propia inteligencia artificial, tiene su origen en el año $1943$, concretamente en el paper A logical calculus of the ideas immanent in nervous activity. En este paper, se describía por primera vez el concepto de una célula cerebral artificial, un análogo simplificado e inspirado por el comportamiento de las neuronas biológicas. Más tarde, en $1957$, se introduciría el perceptrón (The Perceptron — A Perceiving and Recognizing Automaton).
Un algoritmo con la característica de poder “aprender”.
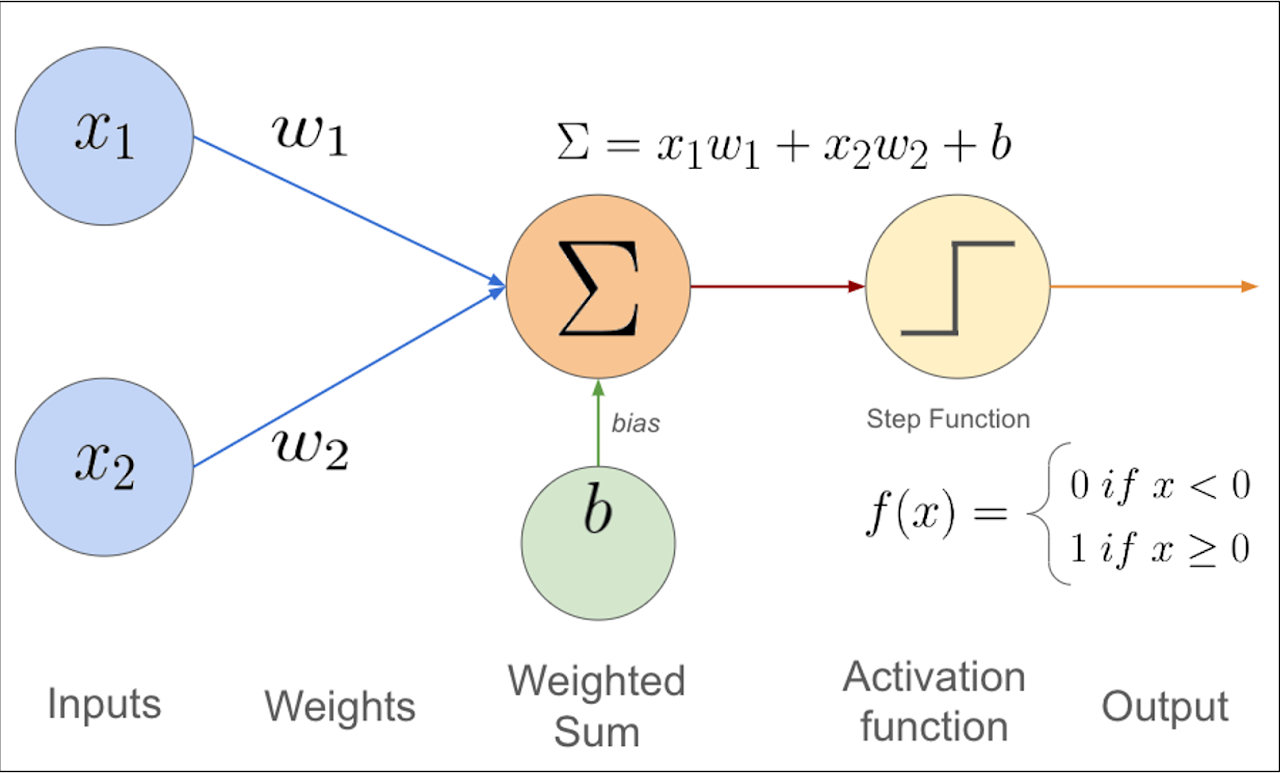
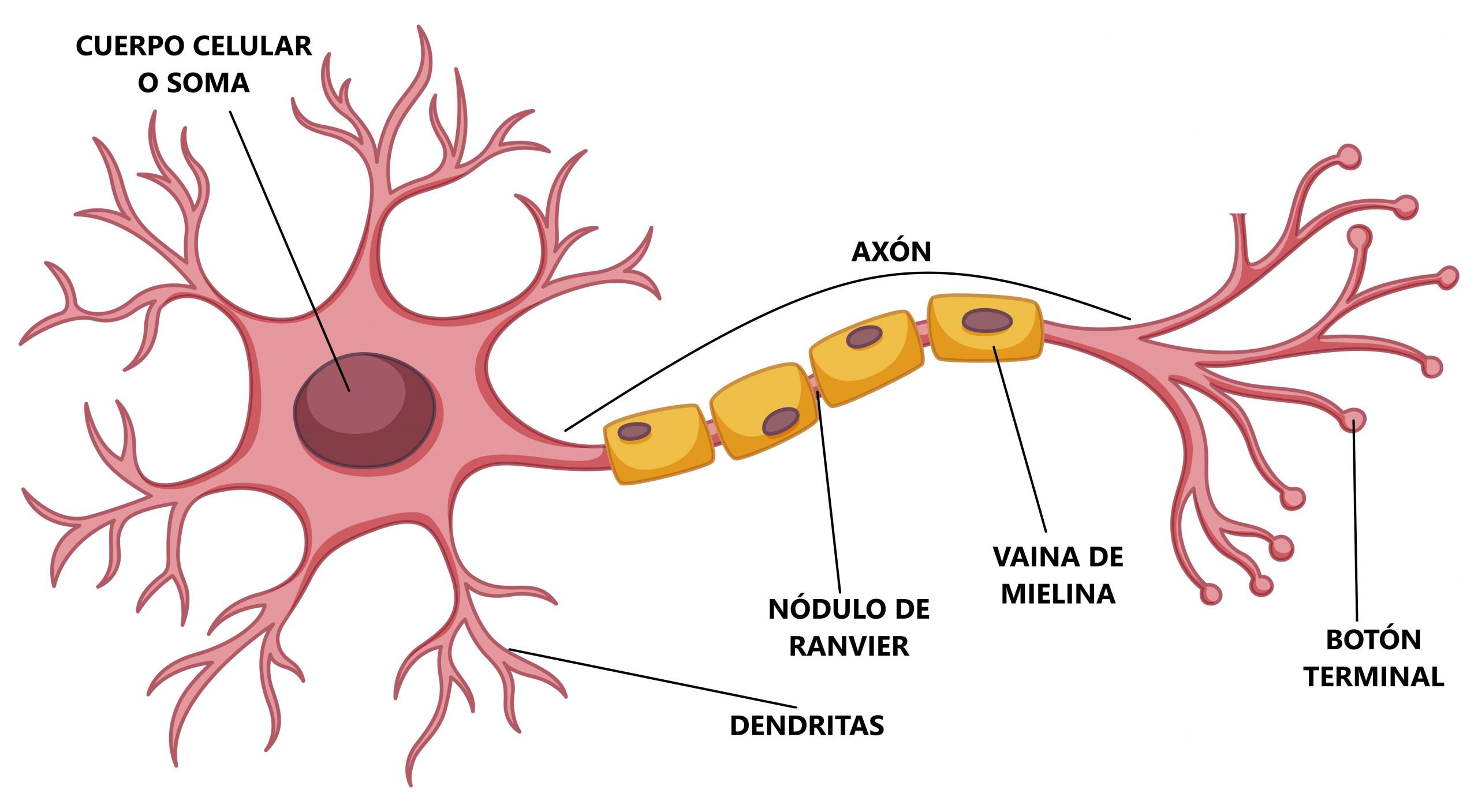
El perceptrón se inspira en cómo funcionan (de forma simplificada) las neuronas biológicas. Estas reciben varias entradas en forma de señales de otras neuronas por las dendritas. Cada señal tiene un peso y la neurona se encarga de sumar todas ellas y procesarlas internamente. Cuando la señal supera un umbral, la neurona manda un impulso eléctrico llamado potencial de acción. Esto es literalmente una onda eléctrica que viaja por el axón y que envía la señal a otras neuronas.
El perceptrón usa esa inspiración y la utiliza para poder aprender. Concretamente, para poder clasificar. El perceptrón es un clasificador lineal binario por naturaleza. El hecho de que sea lineal implica que es capaz de separar los datos únicamente mediante una frontera de decisión lineal. Traza una línea (en dos dimensiones), un plano (en tres dimensiones) o un hiperplano (en dimensiones superiores) que divide el espacio en dos regiones, asignando cada una a una clase distinta.
Matemáticas del perceptrón
Definamos qué es un perceptrón a nivel matemático, de forma sencilla. El perceptrón trabaja como clasificador binario, por tanto se tienen dos clases.
Se define una función de decisión $\sigma(z)$ que combina linealmente las entradas (señales de las dendritas) con un vector de pesos $w$ (la fuerza de cada señal). Los pesos son parámetros que se irán aprendiendo a medida que el algoritmo avance de iteración en iteración:
\[z=w_1x_1+w_2x_2+...+w_nx_n\] \[\begin{equation}\sigma(z)=\begin{cases}1 & \text{if z} \ge \theta \\ -1 & \text{en otro caso}\end{cases}\end{equation}\]Si esa combinación supera un umbral, clasifica como $1$, en caso contrario clasifica como $-1$.
Como ese umbral no lo conocemos, podemos integrarlo a la fórmula como otro parámetro más, otra variable aprendible. De esta forma también simplificamos el código:
\[z\ge\theta \hspace{3mm}\rightarrow\hspace{3mm} z-\theta\ge 0\]Definiendo de esta forma el sesgo o bias:
\[b=-\theta\]Ahora, la combinación lineal quedaría como $z=w_1x_1+w_2x_2+…+w_nx_n + b$, que es, escribiéndolo en forma vectorial, $w^Tx + b$.
¿Por qué esas fórmulas?
Quizá la elección de la fórmula que usa el perceptrón parezca arbitraria, pero nada más alejado de la realidad. Se trata de un clasificador binario, como he mencionado anteriormente. Este clasificador va a tratar de discriminar los puntos del espacio (nuestros datos) en dos regiones. Para ello, ¿qué herramienta matemática nos es más adecuada? A continuación dejo la siguiente imagen:
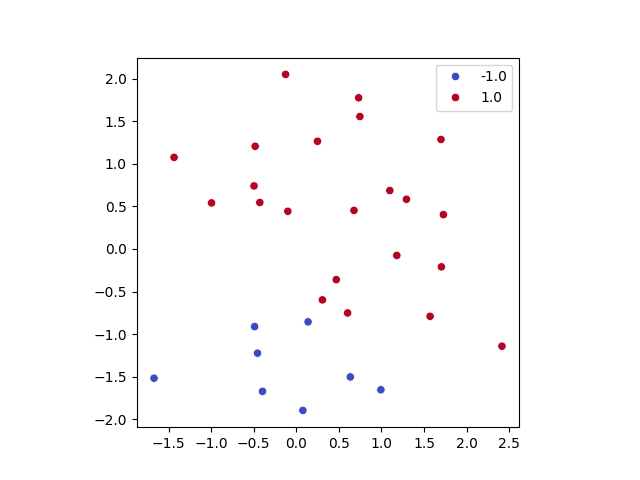
En este sencillo ejemplo hay datos de la clase uno y la clase menos uno. Podrían ser gato y perro, crédito concedido o rechazado, apto o no apto, eso da igual. Lo importante es intentar separarlos de la mejor forma posible y creo no estar muy equivocado ni muy loco si lo intento hacer con una línea recta. Si esto lo extrapolamos al espacio $3D$, es fácil imaginar que la mejor manera (para estos datos que son linealmente separables) es usar un plano. Para todas las dimensiones ocurre lo mismo (asumiendo, y no quiero ser pesado, que son datos linealmente separables). Nuestra frontera de decisión la va a decidir un hiperplano de $N$ dimensiones. La suma ponderada descrita anteriormente coincide con la ecuación del hiperplano en $N$ dimensiones. Para el caso de la recta en el espacio $2D$ es exactamente $w_1x_1+w_2x_2+b=0$, donde el sesgo $b$ es la intersección de la recta con el eje $y$.
La combinación de pesos con entradas es sencilla de entender, igual que la función de clasificación. A la hora de simplificar la fórmula, lo único que hemos hecho es restar el umbral en ambos términos, de forma que $z-\theta$ tiene que ser mayor que cero para clasificar. Así añadimos un parámetro que era desconocido a nuestra fórmula para poder aprenderlo.
En cuanto a la forma vectorial de expresar la combinación de entradas con pesos, recordemos que un vector puede interpretarse como una matriz de una sola fila o de una sola columna. Pongamos que tenemos un vector fila, es decir, tiene dimensiones $1\times N$, donde $N$ es el número de elementos del vector. Si fuese un vector columna, tendría dimensiones $N\times 1$. El nombre columna o fila hace referencia a la forma visual de representarlos: un vector fila se escribe horizontalmente y un vector columna verticalmente.
En el perceptrón solemos considerar $x$ como vector columna de dimensión $N\times 1$ y $w$ también como vector columna de dimensión $N\times 1$. Para poder multiplicarlos y obtener un escalar, transponemos $w$, de forma que $w^T$ pasa a tener dimensión $1\times N$. Así, el producto $w^Tx$ tiene dimensiones $(1\times N)(N\times 1)$ y su resultado es un único valor (un escalar), que coincide con la suma ponderada de las entradas. Finalmente, al añadir el sesgo $b$, obtenemos la expresión completa $z = w^Tx + b$.
Multiplicación paso a paso (producto escalar) con un ejemplo básico
Sea:
\[w=\begin{pmatrix} w_1 \\ w_2 \end{pmatrix}, \qquad x=\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}.\]Primero transponemos $w$:
\[w^T=\begin{pmatrix} w_1 & w_2 \end{pmatrix}.\] \[w^Tx= \begin{pmatrix} w_1 & w_2 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}.\]La regla de multiplicación es “fila por columna”:
\[w^Tx = w_1x_1 + w_2x_2.\]Si añadimos el sesgo, queda:
\[z = w^Tx + b = w_1x_1 + w_2x_2 + b.\]De hecho, podemos simplificar aún más la expresión si tratamos al sesgo como un peso extra que multiplica a una entrada fija. Añadamos el sesgo como un peso $w_0$. Para ello el vector de entradas debe tener un elemento correspondiente, para que las matemáticas funcionen. Por eso añadimos $1$ como $x_0$. Ahora $w=[w_0,w_1,\dots,w_n]$ y $x=[1,x_1,\dots,x_n]$. Ahora la combinación lineal es más simple aún:
\[z=w^Tx\]¿Cómo aprende el perceptrón?
Para que el perceptrón aprenda a dividir el espacio en dos, comienza con unos pesos aleatorios y va iterando sobre los datos.
En cada paso busca un punto que esté mal clasificado. Si lo encuentra, ajusta los pesos para corregir ese error.
La regla de actualización es:
\[w_{new} = w_{old} + y_i x_i\]donde:
- $x_i$ es el punto mal clasificado,
- $y_i \in {-1, +1}$ es su etiqueta correcta.
Solo se actualiza cuando el punto está mal clasificado, es decir, cuando:
\[y_i (w^T x_i) \le 0\]Debemos saber que el vector $w$ es perpendicular a todos los vectores contenidos en el hiperplano de decisión, o lo que es lo mismo, $w$ es el vector normal del hiperplano. Esto es así ya que el hiperplano está definido por la ecuación:
\[w^T x + b = 0\]Tomemos dos puntos cualesquiera $x_1$ y $x_2$ que estén sobre el hiperplano. Entonces se cumple:
\[w^T x_1 + b = 0\] \[w^T x_2 + b = 0\]Si restamos ambas expresiones obtenemos:
\[w^T (x_1 - x_2) = 0\]El vector $(x_1 - x_2)$ es un vector contenido en el hiperplano (porque conecta dos puntos del propio plano). Y si el producto escalar entre $w$ y ese vector es cero, significa que son perpendiculares. De hecho podríamos incluso sacar el ángulo que forma $w$ con el hiperplano y veríamos que es de $90º$. Geométricamente esto es muy importante ya que cambiar la dirección de $w$ implica rotar el hiperplano. Por tanto, cambiar $w$ significa cambiar la orientación de la frontera que separa las clases.
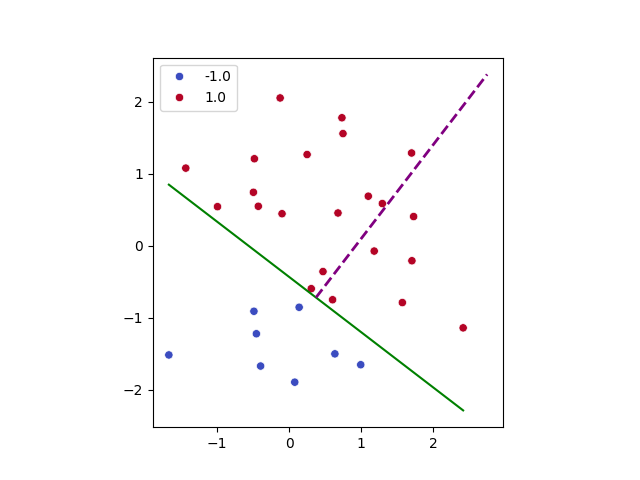
La actualización:
\[w_{new} = w_{old} + y_i x_i\]lo que hace es mover ligeramente el vector $w$ en la dirección necesaria para corregir el error. Veamos los dos casos.
Si el punto es positivo ($y_i = +1$) y está mal clasificado
La actualización se convierte en:
\[w_{new} = w_{old} + x_i\]Estamos sumando el vector del punto a los pesos. Eso hace que $w$ se mueva en dirección hacia ese punto. Como el hiperplano es perpendicular a $w$, la frontera gira ligeramente para intentar dejar ese punto en el lado correcto.
Si el punto es negativo ($y_i = -1$) y está mal clasificado
La actualización se convierte en:
\[w_{new} = w_{old} - x_i\]Ahora estamos restando el vector del punto. Eso mueve $w$ en dirección opuesta al punto negativo, haciendo que la frontera se ajuste para empujarlo al lado correcto.
El perceptrón esconde las matemáticas base que hacen posible aprender. Obviamente los métodos se han perfeccionado iteración tras iteración, pero la base de modelos como GPT es nada más y nada menos que esa. Vincular conceptos geométricos como la ecuación del plano y de la recta a modelos de inteligencia artificial tan potentes, capaces de simular el lenguaje humano, hacen explotar muchas cabezas y silenciar muchas bocas que decían: ¿pero para qué sirven estas tonterías que aprendemos en mates?
Dejo finalmente una pequeña simulación hecha por Claude para ver cómo se ajusta la frontera de decisión: